Neocijenjeno
6. prosinca 2012. 17:11 (13 godine, 2 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
sluzbeno rjesenje ( http://vinkovic.org/Projects/MindExercises/matematika/2001-zup-1234ss.pdf ) kaze da prvi igrac pobjedjuje tako da prvi potez stavi u centralno polje a dalje igra centralno simetricno.
ja mislim da je to krivo
sta ako drugi igrac igra u srednji redak, tako da nakon 1000 poteza prvoga i 999 poteza drugoga je taj srednji redak (x, 1001) (koji se centralnosimetricno preslikava u samog sebe) skroz popunjen osim prvog i zadnjeg polja. Onda sljedecih 1000 poteza popuni gornju polovicu prvog stupca (1, y) (dok 1. igrac popuni donju polovicu najdesnijeg). sljedeci potez postavi npr u (1, 1002), prvi centralnosimetricno. i sada je u retku i stupcu od (1, 1001) ostalo 999+2=1001 polja dakle drugi moze odigrat potez ali prvi ne moze centralnosimetricno. (radio sam da se polje broji u onih 1000 u retku i stupcu, al analogno je ako se ne broji)
jesam glup ja ili sluzbeno rjesenje? :D
ja mislim da je to krivo
sta ako drugi igrac igra u srednji redak, tako da nakon 1000 poteza prvoga i 999 poteza drugoga je taj srednji redak (x, 1001) (koji se centralnosimetricno preslikava u samog sebe) skroz popunjen osim prvog i zadnjeg polja. Onda sljedecih 1000 poteza popuni gornju polovicu prvog stupca (1, y) (dok 1. igrac popuni donju polovicu najdesnijeg). sljedeci potez postavi npr u (1, 1002), prvi centralnosimetricno. i sada je u retku i stupcu od (1, 1001) ostalo 999+2=1001 polja dakle drugi moze odigrat potez ali prvi ne moze centralnosimetricno. (radio sam da se polje broji u onih 1000 u retku i stupcu, al analogno je ako se ne broji)
jesam glup ja ili sluzbeno rjesenje? :D
Komentari:
kokan, 9. prosinca 2012. 16:37
mislim da je sve u redu sa zadatkom. nakon sto igrac A odigra prvi potez na sredisnje polje, na svaki potez 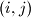 igraca B igrac A moze odigrati potez
igraca B igrac A moze odigrati potez 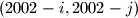 . vjerojatno vas buni situacija kada igrac B odigra potez oblika
. vjerojatno vas buni situacija kada igrac B odigra potez oblika 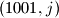 ili
ili 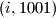 . u tom ce slucaju igrac A odigrati
. u tom ce slucaju igrac A odigrati 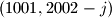 ili
ili 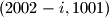 cime se broj slobodnih polja u 1001. retku/stupcu smanjuje za
cime se broj slobodnih polja u 1001. retku/stupcu smanjuje za  . kako je igrac A na pocetku odigrao
. kako je igrac A na pocetku odigrao 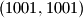 , broj slobodnih polja u 1001. retku i 1001. stupcu je
, broj slobodnih polja u 1001. retku i 1001. stupcu je 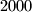 i nakon svaka dva poteza ce se ocuvati parnost.
i nakon svaka dva poteza ce se ocuvati parnost.
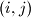 igraca B igrac A moze odigrati potez
igraca B igrac A moze odigrati potez 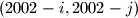 . vjerojatno vas buni situacija kada igrac B odigra potez oblika
. vjerojatno vas buni situacija kada igrac B odigra potez oblika 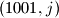 ili
ili 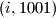 . u tom ce slucaju igrac A odigrati
. u tom ce slucaju igrac A odigrati 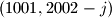 ili
ili 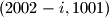 cime se broj slobodnih polja u 1001. retku/stupcu smanjuje za
cime se broj slobodnih polja u 1001. retku/stupcu smanjuje za  . kako je igrac A na pocetku odigrao
. kako je igrac A na pocetku odigrao 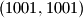 , broj slobodnih polja u 1001. retku i 1001. stupcu je
, broj slobodnih polja u 1001. retku i 1001. stupcu je 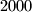 i nakon svaka dva poteza ce se ocuvati parnost.
i nakon svaka dva poteza ce se ocuvati parnost. Zadnja promjena: kokan, 9. prosinca 2012. 16:38
ogi, 7. prosinca 2012. 18:11
grga, 7. prosinca 2012. 00:27
mimaro, 6. prosinca 2012. 17:57
mimaro, 6. prosinca 2012. 17:51
 Školjka
Školjka 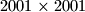 . Igrač može staviti pješaka na prazno mjesto na ploči ako i samo ako u pripadnom retku i stupcu zajedno, ima više od
. Igrač može staviti pješaka na prazno mjesto na ploči ako i samo ako u pripadnom retku i stupcu zajedno, ima više od 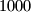 slobodnih mjesta. Gubi onaj igrač koji ne može staviti pješaka. Koji igrač ima pobjedničku strategiju?
slobodnih mjesta. Gubi onaj igrač koji ne može staviti pješaka. Koji igrač ima pobjedničku strategiju?