Točno
25. travnja 2017. 22:19 (8 godine, 10 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
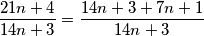
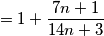 Ako je razlomak
Ako je razlomak 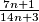 neskrativ, neskrativ je i
neskrativ, neskrativ je i 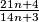 jer je GCD(a+b, a) = GCD(a, b) po Euklidovom algoritmu, znaci ako dokazemo da je
jer je GCD(a+b, a) = GCD(a, b) po Euklidovom algoritmu, znaci ako dokazemo da je 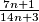 neskrativ, dokazali smo i da je
neskrativ, dokazali smo i da je 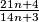 neskrativ. Neka je x = 7n + 1. Onda je
neskrativ. Neka je x = 7n + 1. Onda je 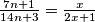 , a po Euklidovom algoritmu GCD(2x + 1, x) = GCD(x + 1, x) = GCD(1, x) = 1, a buduci da je najveci zajednicki djelitelj brojnika i nazivnika razlomka 1, razlomak
, a po Euklidovom algoritmu GCD(2x + 1, x) = GCD(x + 1, x) = GCD(1, x) = 1, a buduci da je najveci zajednicki djelitelj brojnika i nazivnika razlomka 1, razlomak 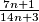 je neskrativ, pa je neskrativ i
je neskrativ, pa je neskrativ i 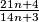 , sto je trebalo dokazati.
, sto je trebalo dokazati.
 Školjka
Školjka 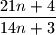 is irreducible for every natural number
is irreducible for every natural number  .
.