Točno
17. travnja 2012. 20:49 (13 godine, 10 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Možemo primjetiti da je 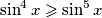 i
i 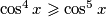 .
.
Dakle, dovoljno je dokazati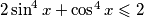 .
.
Također, primijetimo da je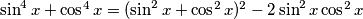 .
.
Uvrštavanjem i sređivanjem dobivamo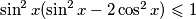 što sigurno vrijedi jer su oba broja manja ili jednaka 1.
što sigurno vrijedi jer su oba broja manja ili jednaka 1.
Jednakost se za drugi izraz postiže za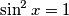 pa je za početni izraz dovoljno provjeriti te slučajeve.
pa je za početni izraz dovoljno provjeriti te slučajeve.
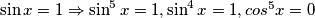 , pa vidimo da za
, pa vidimo da za 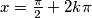 jednakost vrijedi.
jednakost vrijedi.
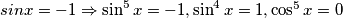 , za što jednakost ne vrijedi, pa vidimo da se jednakost postiže jedino za
, za što jednakost ne vrijedi, pa vidimo da se jednakost postiže jedino za 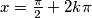 .
.
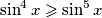 i
i 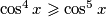 .
.Dakle, dovoljno je dokazati
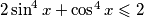 .
.Također, primijetimo da je
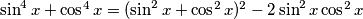 .
.Uvrštavanjem i sređivanjem dobivamo
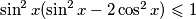 što sigurno vrijedi jer su oba broja manja ili jednaka 1.
što sigurno vrijedi jer su oba broja manja ili jednaka 1.Jednakost se za drugi izraz postiže za
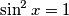 pa je za početni izraz dovoljno provjeriti te slučajeve.
pa je za početni izraz dovoljno provjeriti te slučajeve.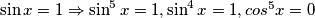 , pa vidimo da za
, pa vidimo da za 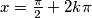 jednakost vrijedi.
jednakost vrijedi.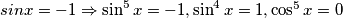 , za što jednakost ne vrijedi, pa vidimo da se jednakost postiže jedino za
, za što jednakost ne vrijedi, pa vidimo da se jednakost postiže jedino za 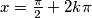 .
.  Školjka
Školjka 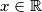 vrijedi nejednakost
vrijedi nejednakost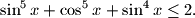
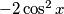 u zagradi.. ? inace je ok
u zagradi.. ? inace je ok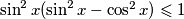 što sigurno vrijedi jer su oba broja manja ili jednaka 1.
što sigurno vrijedi jer su oba broja manja ili jednaka 1.