Točno
23. srpnja 2017. 20:58 (8 godine, 7 mjeseci)
In a plane the circles 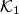 and
and 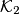 with centers
with centers 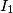 and
and 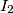 , respectively, intersect in two points
, respectively, intersect in two points  and
and  . Assume that
. Assume that 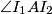 is obtuse. The tangent to
is obtuse. The tangent to 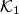 in
in  intersects
intersects 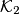 again in
again in  and the tangent to
and the tangent to 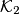 in
in  intersects
intersects 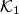 again in
again in  . Let
. Let 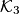 be the circumcircle of the triangle
be the circumcircle of the triangle 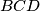 . Let
. Let  be the midpoint of that arc
be the midpoint of that arc  of
of 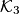 that contains
that contains  . The lines
. The lines  and
and  intersect
intersect 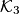 again in
again in  and
and  , respectively. Prove that the line
, respectively. Prove that the line  is perpendicular to
is perpendicular to 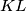 .
.
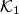 and
and 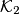 with centers
with centers 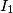 and
and 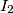 , respectively, intersect in two points
, respectively, intersect in two points  and
and  . Assume that
. Assume that 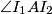 is obtuse. The tangent to
is obtuse. The tangent to 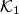 in
in  intersects
intersects 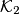 again in
again in  and the tangent to
and the tangent to 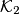 in
in  intersects
intersects 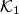 again in
again in  . Let
. Let 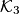 be the circumcircle of the triangle
be the circumcircle of the triangle 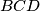 . Let
. Let  be the midpoint of that arc
be the midpoint of that arc  of
of 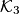 that contains
that contains  . The lines
. The lines  and
and  intersect
intersect 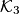 again in
again in  and
and  , respectively. Prove that the line
, respectively. Prove that the line  is perpendicular to
is perpendicular to 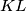 .
. Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
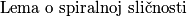 : Ako su dane u ravnini točke
: Ako su dane u ravnini točke 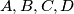 i
i  sjecište pravaca
sjecište pravaca  i
i  tada je sjecište kružnica
tada je sjecište kružnica 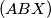 i
i 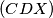 centar spiralne simetrije
centar spiralne simetrije  za koju je
za koju je 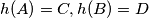 . (*)
. (*)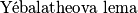 : Ako su dane kružnice
: Ako su dane kružnice 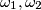 centara
centara 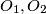 i sjecišta
i sjecišta 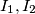 tada je
tada je 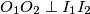 . (**)
. (**)Neka je
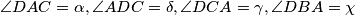 .
.Primjenom (*) za
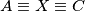 znamo da je
znamo da je  centar spiralne sličnosti koja šalje
centar spiralne sličnosti koja šalje  u
u  i
i  u
u  . Stoga
. Stoga 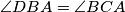 ,
, 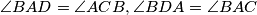 . Po zbroju kutova u četverokutu
. Po zbroju kutova u četverokutu 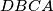 imamo
imamo 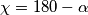 te iz toga
te iz toga 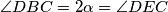 . Uz to te kako se
. Uz to te kako se  nalazi na simetrali dužine
nalazi na simetrali dužine  zaključujemo da je
zaključujemo da je  centar kružnice
centar kružnice 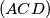 .
.Nadalje neka je
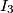 centar kružnice
centar kružnice 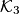 i
i  sjecište
sjecište  i
i 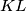 . Po (**) imamo
. Po (**) imamo 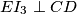 , a kako želimo dokazati
, a kako želimo dokazati 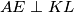 dovoljno je dokazati
dovoljno je dokazati 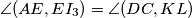 odnosno
odnosno 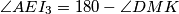 .
.To lako dovršavamo angle chasingom. Kako je
 središte
središte 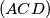 je
je 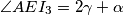 . Također zbog tetivnosti i zbroja u trokutu
. Također zbog tetivnosti i zbroja u trokutu 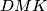 je
je 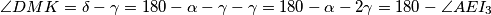 .
. 
Ocjene: (1)
Komentari:
tuksy, 8. kolovoza 2017. 19:19
Poštovani kolega rhldj,
vaše rješenje uistinu jest točno, međutim izgleda da ste pri rješavanju zamijenili K i L. Malen previd, ukoliko bi uz rješenje bila priložena skica bio bi potpuno zanemariv, međutim u ovakvom formatu to postaje znatan problem. Također ste napravili jedan manji tipfeler; naime napisali ste DBA =
DBA =  BCA umjesto
BCA umjesto  DBA =
DBA =  ABC. Također, čini se da ste bez objašnjenja pretpostavili
ABC. Također, čini se da ste bez objašnjenja pretpostavili 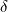 -
- > 0? Opet, nije velika greška jer samo nedostaje kratko objašnjenje zašto to možemo pretpostaviti. Također, u sljedećoj rečenici loše je definirano kako se primjenjuje lema (*): "Primjenom (*) za A
> 0? Opet, nije velika greška jer samo nedostaje kratko objašnjenje zašto to možemo pretpostaviti. Također, u sljedećoj rečenici loše je definirano kako se primjenjuje lema (*): "Primjenom (*) za A  X
X  C znamo da je B centar spiralne sličnosti koja šalje D u A i A u C."
C znamo da je B centar spiralne sličnosti koja šalje D u A i A u C."
Rješenje je točno, ali molim da ispravite navedene greške i poradite na svom zapisivanju rješenja.
S poštovanjem,
Dipl. ing. MEMO-a tuksy
vaše rješenje uistinu jest točno, međutim izgleda da ste pri rješavanju zamijenili K i L. Malen previd, ukoliko bi uz rješenje bila priložena skica bio bi potpuno zanemariv, međutim u ovakvom formatu to postaje znatan problem. Također ste napravili jedan manji tipfeler; naime napisali ste
 DBA =
DBA =  BCA umjesto
BCA umjesto  DBA =
DBA =  ABC. Također, čini se da ste bez objašnjenja pretpostavili
ABC. Također, čini se da ste bez objašnjenja pretpostavili 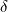 -
- > 0? Opet, nije velika greška jer samo nedostaje kratko objašnjenje zašto to možemo pretpostaviti. Također, u sljedećoj rečenici loše je definirano kako se primjenjuje lema (*): "Primjenom (*) za A
> 0? Opet, nije velika greška jer samo nedostaje kratko objašnjenje zašto to možemo pretpostaviti. Također, u sljedećoj rečenici loše je definirano kako se primjenjuje lema (*): "Primjenom (*) za A  X
X  C znamo da je B centar spiralne sličnosti koja šalje D u A i A u C."
C znamo da je B centar spiralne sličnosti koja šalje D u A i A u C." Rješenje je točno, ali molim da ispravite navedene greške i poradite na svom zapisivanju rješenja.
S poštovanjem,
Dipl. ing. MEMO-a tuksy
 Školjka
Školjka