Točno
27. srpnja 2017. 12:35 (8 godine, 7 mjeseci)
niz
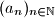
je zadan rekurzivno s
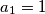
,
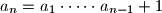
, za

.
odredite najmanji realni broj

takav da je
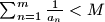
za svaki
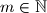
.
%V0
niz $(a_n)_{n\in\mathbb{N}}$ je zadan rekurzivno s $a_1 = 1$,
$a_n = a_1 \cdot \dots \cdot a_{n-1} + 1$, za $n \geq 2$.
odredite najmanji realni broj $M$ takav da je
$\sum_{n=1}^m \frac{1}{a_n} < M$ za svaki $m \in \mathbb{N}$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Primjetimo da je
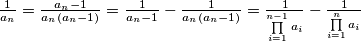
Jasno je da će nakon što se sve lijepo pokrati vrijediti:
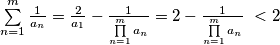
za svaki
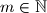
.
Budući da izraz
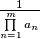
neprestano raste(što je veći broj

) i teži ka nuli,
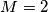
je najmanji takav broj

%V0
Primjetimo da je
$\frac{1}{a_n} = \frac{a_n -1}{a_n(a_n -1)} = \frac{1}{a_n -1} - \frac{1}{a_n(a_n -1)} = \frac{1}{ \prod \limits_{i=1}^{n-1} a_i} - \frac{1}{ \prod \limits_{i=1}^n a_i}$
Jasno je da će nakon što se sve lijepo pokrati vrijediti:
$\sum \limits_{n=1}^m { \frac{1}{a_n}} = \frac{2}{a_1} - \frac{1}{ \prod \limits_{n=1}^m a_n} = 2 - \frac{1}{ \prod \limits_{n=1}^m a_n} \ < 2$ za svaki $m \in \mathbb{N}$.
Budući da izraz $\frac{1}{ \prod \limits_{n=1}^m a_n}$ neprestano raste(što je veći broj $m$) i teži ka nuli, $M=2$ je najmanji takav broj $M$