Točno
19. kolovoza 2017. 18:43 (8 godine, 6 mjeseci)
Find all functions
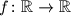
such that the equality
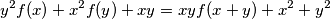
holds for all
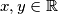
, where
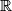
is the set of real numbers.
%V0
Find all functions $f \colon \mathbb R \to \mathbb R$ such that the equality $$y^2f(x) + x^2f(y) + xy = xyf(x + y) + x^2 + y^2$$ holds for all $x, y \in \Bbb R$, where $\Bbb R$ is the set of real numbers.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Uvrstimo li u početnu jednadžbu vrijednost
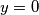
dobijamo
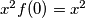
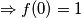
Uvedimo funkciju
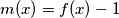
, tada vrijedi
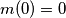
, a početna jednakost postaje:
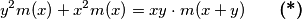
Neka
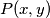
označava uvrštavanje varijabli
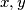
u
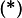
.
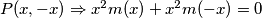
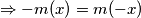
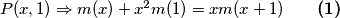
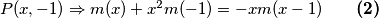
Ako u
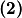
zamijenimo
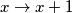
dobivamo:
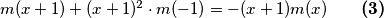
Ako iz
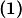
i
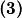
izjednačimo
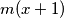
i iskoristimo
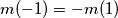
dobivamo:
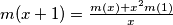
i
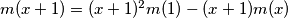
odakle sređivanjem slijedi
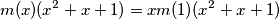
a budući da je
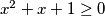
za svaki
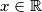
vrijedi
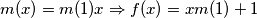
. Ako
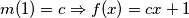
što uvrštavanjem u početnu jednakost zaista jest rješenje.
%V0
Uvrstimo li u početnu jednadžbu vrijednost $y=0$ dobijamo $x^2 f(0) = x^2$ $ \Rightarrow f(0) = 1$
Uvedimo funkciju $ m(x) = f(x) - 1$ \, tada vrijedi $m(0) = 0$ \, a početna jednakost postaje: $$ y^2m(x) + x^2m(x) = xy \cdot m(x+y) \qquad \textbf{(*)}$$
Neka $P(x,y)$ označava uvrštavanje varijabli $x,y$ u $\textbf{(*)}$.
$P(x,-x) \Rightarrow x^2 m(x) + x^2 m(-x) = 0$ $ \Rightarrow -m(x) = m(-x)$
$P(x,1) \Rightarrow m(x) + x^2 m(1) = xm(x+1) \qquad \textbf{(1)}$
$P(x, -1) \Rightarrow m(x) + x^2 m(-1) = -x m(x-1) \qquad \textbf{(2)}$
Ako u $ \textbf{(2)}$ zamijenimo $x \rightarrow x+1$ dobivamo:
$m(x+1) + (x+1)^2 \cdot m(-1) = -(x+1) m(x) \qquad \textbf{(3)}$
Ako iz $\textbf{(1)}$ i $\textbf{(3)}$ izjednačimo $m(x+1)$ i iskoristimo $ m(-1) = -m(1)$ dobivamo:
$m(x+1) = \frac{m(x) + x^2 m(1)}{x}$ i $m(x+1) = (x+1)^2 m(1) - (x+1)m(x)$ odakle sređivanjem slijedi $$m(x) (x^2 + x + 1) = x m(1)(x^2 + x + 1)$$ a budući da je $x^2 + x + 1 \geq 0$ za svaki $ x \in \mathbb{R}$ vrijedi $m(x) = m(1)x \Rightarrow f(x) = x m(1) +1$. Ako $m(1) = c \Rightarrow f(x) = cx + 1$ što uvrštavanjem u početnu jednakost zaista jest rješenje.
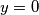 dobijamo
dobijamo 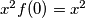
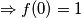
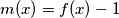 , tada vrijedi
, tada vrijedi 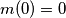 , a početna jednakost postaje:
, a početna jednakost postaje: 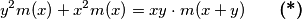
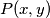 označava uvrštavanje varijabli
označava uvrštavanje varijabli 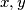 u
u 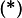 .
.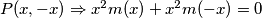
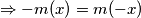
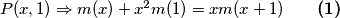
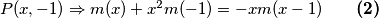
 zamijenimo
zamijenimo 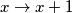 dobivamo:
dobivamo: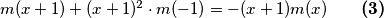
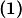 i
i 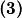 izjednačimo
izjednačimo 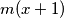 i iskoristimo
i iskoristimo 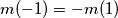 dobivamo:
dobivamo: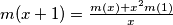 i
i 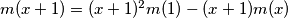 odakle sređivanjem slijedi
odakle sređivanjem slijedi 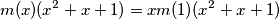 a budući da je
a budući da je 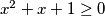 za svaki
za svaki 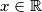 vrijedi
vrijedi 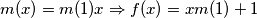 . Ako
. Ako 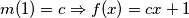 što uvrštavanjem u početnu jednakost zaista jest rješenje.
što uvrštavanjem u početnu jednakost zaista jest rješenje. 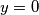 dobijamo
dobijamo 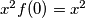
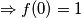
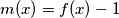 , tada vrijedi
, tada vrijedi 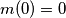 , a početna jednakost postaje:
, a početna jednakost postaje: 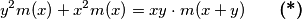
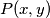 označava uvrštavanje varijabli
označava uvrštavanje varijabli 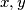 u
u 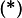 .
.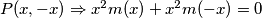
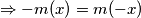
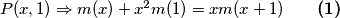
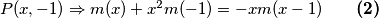
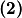 zamijenimo
zamijenimo 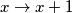 dobivamo:
dobivamo: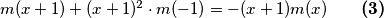
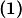 i
i 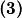 izjednačimo
izjednačimo 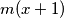 i iskoristimo
i iskoristimo 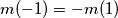 dobivamo:
dobivamo: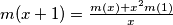 i
i 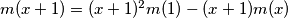 odakle sređivanjem slijedi
odakle sređivanjem slijedi 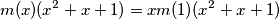 a budući da je
a budući da je 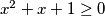 za svaki
za svaki 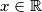 vrijedi
vrijedi 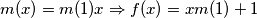 . Ako
. Ako 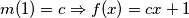 što uvrštavanjem u početnu jednakost zaista jest rješenje.
što uvrštavanjem u početnu jednakost zaista jest rješenje.  Školjka
Školjka 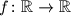 such that the equality
such that the equality 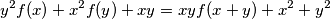 holds for all
holds for all 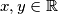 , where
, where 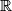 is the set of real numbers.
is the set of real numbers.