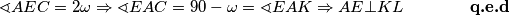Neocijenjeno
20. kolovoza 2017. 12:31 (8 godine, 6 mjeseci)
In a plane the circles
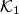
and
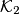
with centers
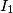
and
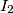
, respectively, intersect in two points

and

. Assume that
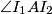
is obtuse. The tangent to
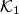
in

intersects
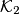
again in

and the tangent to
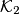
in

intersects
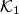
again in

. Let
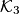
be the circumcircle of the triangle
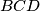
. Let

be the midpoint of that arc

of
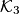
that contains

. The lines

and

intersect
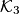
again in

and

, respectively. Prove that the line

is perpendicular to
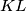
.
%V0
In a plane the circles $\mathcal K_1$ and $\mathcal K_2$ with centers $I_1$ and $I_2$, respectively, intersect in two points $A$ and $B$. Assume that $\angle I_1AI_2$ is obtuse. The tangent to $\mathcal K_1$ in $A$ intersects $\mathcal K_2$ again in $C$ and the tangent to $\mathcal K_2$ in $A$ intersects $\mathcal K_1$ again in $D$. Let $\mathcal K_3$ be the circumcircle of the triangle $BCD$. Let $E$ be the midpoint of that arc $CD$ of $\mathcal K_3$ that contains $B$. The lines $AC$ and $AD$ intersect $\mathcal K_3$ again in $K$ and $L$, respectively. Prove that the line $AE$ is perpendicular to $KL$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Neka su
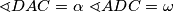
. Zbog kuta tangente i tetive
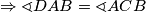
i
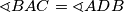
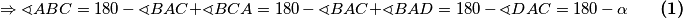
Analogno
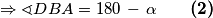
Iz
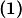
i
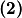
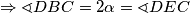
a budući da vrijedi i
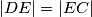
imamo da je

središte opisane kružnice
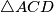
.
Četverokut
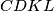
je tetivan, pa vrijedi
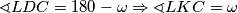
Nadalje
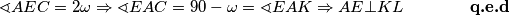
%V0
Neka su $ \sphericalangle DAC = \alpha \,\, \sphericalangle ADC = \omega$. Zbog kuta tangente i tetive $ \Rightarrow \sphericalangle DAB = \sphericalangle ACB$ i $ \sphericalangle BAC = \sphericalangle ADB$ $$ \Rightarrow \sphericalangle ABC = 180\, -\, \sphericalangle BAC + \sphericalangle BCA = 180\, -\, \sphericalangle BAC + \sphericalangle BAD =
180\, -\, \sphericalangle DAC = 180\, -\, \alpha \qquad \textbf{(1)}$$ Analogno $$ \Rightarrow \sphericalangle DBA = 180\, - \, \alpha \qquad \textbf{(2)}$$ Iz $\textbf{(1)}$ i $\textbf{(2)}$ $ \Rightarrow \sphericalangle DBC = 2 \alpha = \sphericalangle DEC$ a budući da vrijedi i $ |DE| = |EC|$ imamo da je $E$ središte opisane kružnice $\triangle ACD$.
Četverokut $CDKL$ je tetivan, pa vrijedi $$ \sphericalangle LDC = 180 - \omega \Rightarrow \sphericalangle LKC = \omega$$ Nadalje $$\sphericalangle AEC = 2 \omega \Rightarrow \sphericalangle EAC = 90 - \omega = \sphericalangle EAK \Rightarrow AE \bot KL \qquad \qquad \textbf{q.e.d}$$
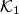 and
and 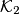 with centers
with centers 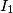 and
and 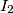 , respectively, intersect in two points
, respectively, intersect in two points  and
and  . Assume that
. Assume that 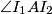 is obtuse. The tangent to
is obtuse. The tangent to 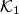 in
in  intersects
intersects 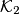 again in
again in  and the tangent to
and the tangent to 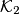 in
in  intersects
intersects 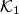 again in
again in  . Let
. Let 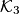 be the circumcircle of the triangle
be the circumcircle of the triangle 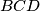 . Let
. Let  be the midpoint of that arc
be the midpoint of that arc  of
of 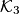 that contains
that contains  . The lines
. The lines  and
and  intersect
intersect 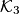 again in
again in  and
and  , respectively. Prove that the line
, respectively. Prove that the line  is perpendicular to
is perpendicular to 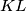 .
. 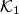 and
and 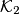 with centers
with centers 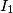 and
and 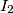 , respectively, intersect in two points
, respectively, intersect in two points  and
and  . Assume that
. Assume that 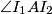 is obtuse. The tangent to
is obtuse. The tangent to 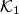 in
in  intersects
intersects 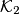 again in
again in  and the tangent to
and the tangent to 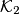 in
in  intersects
intersects 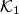 again in
again in  . Let
. Let 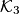 be the circumcircle of the triangle
be the circumcircle of the triangle 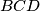 . Let
. Let  be the midpoint of that arc
be the midpoint of that arc  of
of 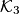 that contains
that contains  . The lines
. The lines  and
and  intersect
intersect 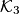 again in
again in  and
and  , respectively. Prove that the line
, respectively. Prove that the line  is perpendicular to
is perpendicular to 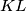 .
.  Školjka
Školjka 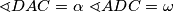 . Zbog kuta tangente i tetive
. Zbog kuta tangente i tetive 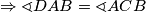 i
i 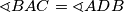
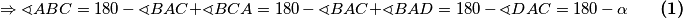 Analogno
Analogno 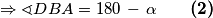 Iz
Iz 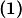 i
i 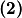
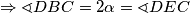 a budući da vrijedi i
a budući da vrijedi i 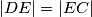 imamo da je
imamo da je 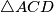 .
.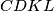 je tetivan, pa vrijedi
je tetivan, pa vrijedi 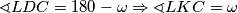 Nadalje
Nadalje