Točno
8. rujna 2017. 14:29 (8 godine, 6 mjeseci)
Nad stranicama

i

kvadrata

konstruirani su jednakostranični trokuti
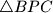
i
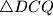
. Dokažite da je trokut
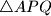
jednakostraničan.
%V0
Nad stranicama $BC$ i $CD$ kvadrata $ABCD$ konstruirani su jednakostranični trokuti $\triangle BPC$ i $\triangle DCQ$. Dokažite da je trokut $\triangle APQ$ jednakostraničan.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kao prvo je ocigledno AQ=AP jer su trokuti ABP i ADQ sukladni (AB=AD, BP=DQ, kutevi ABP=ADQ=150 ). Primijetimo da su ABP i ADQ jednakokračni jer je AB=BC=BP i AC=CD=CQ. Stoga je kut DAQ velicine (180-150)/2=15, isto za BAP. Onda je PAQ=90-15-15=60 pa je APQ jednakostranican jer je jednakokracan i jedan mu je kut 60.
Kao prvo je ocigledno AQ=AP jer su trokuti ABP i ADQ sukladni (AB=AD, BP=DQ, kutevi ABP=ADQ=150 ). Primijetimo da su ABP i ADQ jednakokračni jer je AB=BC=BP i AC=CD=CQ. Stoga je kut DAQ velicine (180-150)/2=15, isto za BAP. Onda je PAQ=90-15-15=60 pa je APQ jednakostranican jer je jednakokracan i jedan mu je kut 60.
| 8. rujna 2017. 15:53 | Lugo | Točno |
 Školjka
Školjka  i
i  kvadrata
kvadrata  konstruirani su jednakostranični trokuti
konstruirani su jednakostranični trokuti 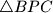 i
i 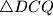 . Dokažite da je trokut
. Dokažite da je trokut 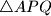 jednakostraničan.
jednakostraničan.