Točno
8. rujna 2017. 16:26 (7 godine, 5 mjeseci)
Za koje cijele brojeve
je
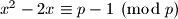
za neki prost broj
?
%V0
Za koje cijele brojeve $x$ je $x^2 -2x \equiv p-1 \pmod p$ za neki prost broj $p$?
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Nadodaj 1 u kongruenciju. Dobivamo da p dijeli x^2-2x+1=(x-1)^2 sto znaci da p dijeli x-1, sto znaci da su trazeni x-evi svi cijeli brojevi čije vrijednosti umanjene za 1 su višekratnici od p. (0, -p, -2p.. isto brojimo kao višekratnike u ovom slučaju).
Nadodaj 1 u kongruenciju.
Dobivamo da p dijeli x^2-2x+1=(x-1)^2 sto znaci da p dijeli x-1, sto znaci da su trazeni x-evi svi cijeli brojevi čije vrijednosti umanjene za 1 su višekratnici od p. (0, -p, -2p.. isto brojimo kao višekratnike u ovom slučaju).
| 8. rujna 2017. 21:51 | miksi | Točno |
Školjka