Kliknite ovdje kako biste prikazali rješenje.
Kvadrati negativnih brojeva su jednaki kvadratima njihovim pozitivnim vrijednostima, pa je dovoljno promatrati prirodne brojeve (nulu i kvadrate svih brojeva djeljivih sa p ću unaprijed brojiti kao jedan mogući modul sa p).
Za kvadrate svih brojeva većih od p već možemo gledati kvadrat njihovih modula sa p, jer su ti ostaci identični, pa ajmo gledati samo kvadrate cijelih brojeva između 1 i p-1 (uključivo). Pronađimo sve jednakosti kongruencija kvadrata tih brojeva.
Da budem detaljniji, gledajmo brojeve x i p-x, 1<=x<=(p-1)/2. Razlika njihovih kvadrata (p-x)^2-x^2=(p-x+x)(p-x-x)=p(p-2x) je djeljiva s p, što znači da su kongruencija kvadrata od x i p-x jednake.
Pretpostavimo da su kvadrati od a i b kongruentni modulo p, 1<=a<b<=p-1. Onda p dijeli b^2-a^2=(b+a)(b-a). Primijetimo da je 1<=b-a<=p-2, pa p ne dijeli b-a, a iz uvjeta da je p prost, saznajemo da p dijeli b+a. Vrijedi 3<=a+b<=2p-3, pa uz p>2 imamo da je a+b=p.
Znači, dokazali smo da su kvadrati svih brojeva u skupu 1,p-1, čiji su zbrojevi p, kongruentni modulo p, a i da su oni jedini. Znači od kongruentnosti vrijedi da je 1^2 kongruentno sa (p-1)^2, 2^2 kongruentno sa (p-2)^2 ... i da je (p-1)^2 kongruentno sa (p+1)^2, no ništa više.
Ukupan broj različitih ostataka onda pri dijeljenju kvadrata cijelih brojeva s prostim brojem p koji je veći od 2, je (p+1)/2 (imamo da je (p-1)/2 za brojeve koji nisu djeljivi s p, zajedno s neparnošću od p, te plus 1 zbog ostatka 0).
 Školjka
Školjka  daju kvadrati cijelih brojeva, za prost broj
daju kvadrati cijelih brojeva, za prost broj 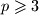 ?
?