Točno
9. rujna 2017. 23:27 (6 godine, 7 mjeseci)
Neka su $c$ i $d$ pozitivni djelitelji prirodnog broja $n$. Ako je $c > d$, dokaži da je $c > d+\dfrac{d^2}{n}$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
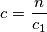
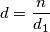
Uz
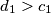
treba pokazati
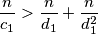
odnosno
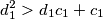
ali uvjet nam daje
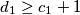
odnosno
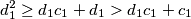
što je i trebalo pokazati.
%V0
$$c = \frac{n}{c_1}$$
$$d = \frac{n}{d_1}$$
Uz $d_1 > c_1$ treba pokazati $$\frac{n}{c_1} > \frac{n}{d_1} + \frac{n}{d_1^2}$$
odnosno $$d_1^2 > d_1c_1 + c_1$$
ali uvjet nam daje $d_1 \geq c_1 + 1$ odnosno $$d_1^2 \geq d_1c_1 + d_1 > d_1c_1 + c_1$$
što je i trebalo pokazati.
| 10. rujna 2017. 10:20 | Lugo | Točno |