Točno
10. rujna 2017. 15:53 (8 godine, 5 mjeseci)
neka je

prirodan broj i neka su
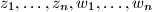
kompleksni brojevi takvi da za svaki izbor brojeva
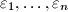
iz skupa
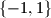
vrijedi
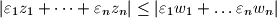
.
dokazite da je
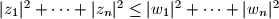
.
%V0
neka je $n$ prirodan broj i neka su $z_1, \dots, z_n, w_1, \dots, w_n$ kompleksni brojevi takvi da za svaki izbor brojeva $\varepsilon_1, \dots, \varepsilon_n$ iz skupa $\{-1, 1\}$ vrijedi
$|\varepsilon_1z_1 + \dots + \varepsilon_nz_n| \leq |\varepsilon_1w_1 + \dots \varepsilon_nw_n|$.
dokazite da je
$|z_1|^2 + \dots + |z_n|^2 \leq |w_1|^2 + \dots + |w_n|^2$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Očekivano rješenje ovog zadatka:
Odaberimo nasumično $\varepsilon_i \in \{-1, 1\}$ s probability $\frac{1}{2}$. Svi $z_i, w_i$ su zadane konstante.
Pretpostavimo da su sve spomenute slučajne varijable identitet.
Tada imamo $\varepsilon_i^2 = 1$ i za $i \neq j$: $$\mathbb{E}[\varepsilon_i\varepsilon_j] = \frac{1\cdot(-1) + (-1)\cdot1 + 1\cdot1 + (-1)\cdot(-1)}{4} = 0$$
Prva nejednakost implicira:
$$ \mathbb{E} \Big[\big | \sum_{i = 1}^n \varepsilon_i z_i \big|^2 - \big | \sum_{i = 1}^n \varepsilon_i w_i \big|^2 \Big] \leq 0$$
$$ \mathbb{E} \Big[\big | \sum_{i = 1}^n \varepsilon_i z_i \big|^2 \Big] \leq \mathbb{E} \Big[\big | \sum_{i = 1}^n \varepsilon_i w_i \big|^2 \Big]$$
$$ \mathbb{E} \Big[\big ( \sum_{i = 1}^n\varepsilon_i z_i \big)( \sum_{i = 1}^n\varepsilon_i \overline{z_i} \big) \Big] \leq \mathbb{E} \Big[\big ( \sum_{i = 1}^n\varepsilon_i w_i \big)( \sum_{i = 1}^n\varepsilon_i \overline{w_i} \big) \Big]$$
$$ \mathbb{E} \Big[\sum_{i=1}^n \varepsilon_i^2|z_i|^2 + \sum_{i \neq j}\varepsilon_i\varepsilon_j(z_i\overline{z_j}+\overline{z_i}z_j)\Big] \leq \mathbb{E} \Big[\sum_{i=1}^n \varepsilon_i^2|w_i|^2 + \sum_{i \neq j}\varepsilon_i\varepsilon_j(w_i\overline{w_j}+\overline{w_i}w_j)\Big]$$
$$\sum_{i=1}^n |z_i|^2 + \sum_{i \neq j} (z_i\overline{z_j}+\overline{z_i}z_j) \cdot \mathbb{E} \Big[\varepsilon_i\varepsilon_j\Big] \leq \sum_{i=1}^n |w_i|^2 + \sum_{i \neq j} (w_i\overline{w_j}+\overline{w_i}w_j) \cdot \mathbb{E} \Big[\varepsilon_i\varepsilon_j\Big] $$
$$\sum_{i=1}^n |z_i|^2 \leq \sum_{i=1}^n |w_i|^2$$
što je i trebalo dokazati.
| 10. rujna 2017. 16:56 | abeker | Točno |