Neocijenjeno
10. rujna 2017. 21:22 (8 godine, 4 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Neka su 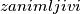 brojevi oni s
brojevi oni s 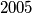 znamenaka koje su sve ili
znamenaka koje su sve ili  ili
ili  i neka su
i neka su 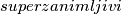 brojevi oni koji su
brojevi oni koji su 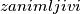 i djeljivi s
i djeljivi s 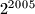
Primijetimo da ima točno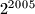
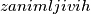 brojeva.
brojeva.
Pokažemo li da svaka dva daju različit ostatak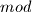
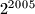 , pokazat ćemo da postoji jedinstven
, pokazat ćemo da postoji jedinstven 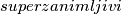 broj.
broj.
Pretpostavimo suprotno i neka su i
i  različiti
različiti 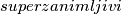 brojevi.
brojevi.
Tada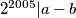 iz čega slijedi da
iz čega slijedi da  i
i  imaju jednake zadnje znamenke i
imaju jednake zadnje znamenke i 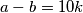 .
.
Ali tada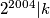 pa opet imamo istu situaciju jer je
pa opet imamo istu situaciju jer je  razlika dvaju
razlika dvaju 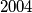 - znamenkastih brojeva sastavljenih od znamenaka
- znamenkastih brojeva sastavljenih od znamenaka  i
i  .
.
Induktivno zaključujemo da su sve znamenke brojeva i
i  jednake čime dobivamo kontradikciju s pretpostavkom da su
jednake čime dobivamo kontradikciju s pretpostavkom da su  i
i  različiti i ovime je dokaz gotov.
različiti i ovime je dokaz gotov.
 brojevi oni s
brojevi oni s 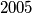 znamenaka koje su sve ili
znamenaka koje su sve ili  ili
ili  i neka su
i neka su 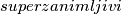 brojevi oni koji su
brojevi oni koji su 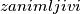 i djeljivi s
i djeljivi s 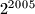
Primijetimo da ima točno
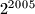
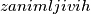 brojeva.
brojeva.Pokažemo li da svaka dva daju različit ostatak
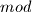
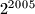 , pokazat ćemo da postoji jedinstven
, pokazat ćemo da postoji jedinstven 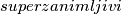 broj.
broj.Pretpostavimo suprotno i neka su
 i
i  različiti
različiti 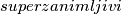 brojevi.
brojevi.Tada
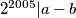 iz čega slijedi da
iz čega slijedi da  i
i  imaju jednake zadnje znamenke i
imaju jednake zadnje znamenke i 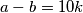 .
.Ali tada
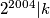 pa opet imamo istu situaciju jer je
pa opet imamo istu situaciju jer je  razlika dvaju
razlika dvaju 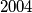 - znamenkastih brojeva sastavljenih od znamenaka
- znamenkastih brojeva sastavljenih od znamenaka  i
i  .
.Induktivno zaključujemo da su sve znamenke brojeva
 i
i  jednake čime dobivamo kontradikciju s pretpostavkom da su
jednake čime dobivamo kontradikciju s pretpostavkom da su  i
i  različiti i ovime je dokaz gotov.
različiti i ovime je dokaz gotov. Komentari:
ikicic, 12. rujna 2017. 18:16
 Školjka
Školjka