Školjka

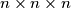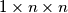$n \times n \times n$ kocka je sastavljena od $n$ "slojeva" $1 \times n \times n$ koji su "zaljepljeni" jedan na drugi. \\ Obojat cemo prvi sloj: \\ 121212.... \\ 343434... \\ 121212... \\ 343434... \\ ... Drugi sloj: \\ 565656... \\ 787878... \\ 565656... \\ 787878... \\ ... Treci sloj kao prvi i tako dalje alternirajuce. Svako stubiste sada sadrzi jednu sredisnju kocku brida 2 i dva 1x1x2 kvadra koji imaju zajednicku stranu 1x2 sa kockom. Vrijedi da u kocki brida 2 se pojavljuje jedinicna kocka svake boje tocno jednom i da su 1x1x2 kvadri oba sacinjena od kocaka 2 boje koje su iste za oba kvadra (npr 3-5 i 3-5). Primijetimo da 1 moze biti u takvom paru sa 2, 3 i 5. (postoji 1x1x2 kvadar s obe boje). Slicno vrijedi za ostale boje dakle ukupno postoji tocno 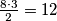$\frac{8 \cdot 3}{2} = 12$ parova tj. 12 razlictih stubista s obziron na broj polja svake boje. \\ Oznacimo s 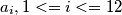$a_i, 1<= i <= 12$ broj odgovarajucih stubista. Ako 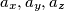$a_x, a_y, a_z$ oznacavaju brojeve stubista koje sadrze boju 1 tada definiramo 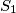$S_1$ kao sumu ta tri broja i analogno za ostalih 8 boja. 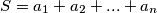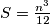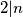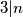Takoder neka je $S = a_1+a_2+...+a_n$\\ Vrijedi $S = \frac{n^3}{12}$ sto implicira $2 |n$ i $3 |n$ Slijedi da se svaka boja pojavljuje tocno 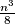$\frac{n^3}{8}$ puta. Zato: \\ $S + 2S_1= \frac{n^3}{8}$\\ $S + 2S_2 = \frac{n^3}{8}$\\ ... 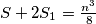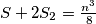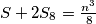\\ $S + 2S_8 = \frac{n^3}{8}$ \\ sto zajedno implicira 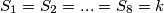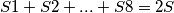$S_1 = S_2 = ... = S_8 = k$ $S1 + S2 + ... + S8 = 2S$ jer svako stubiste se pojavljuje u tocno dvije sume (ima dva kvadra 1x1x2 sa tocno 2 boje). \\ Dakle 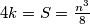$4k = S = \frac{n^3}{8}$, slijedi 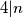$4|n$ Dakle nuzan uvijet za postojanje poplocavanja je 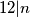$12 | n$. Da je i dovoljan pokazat cemo konstrukcijom. Primijetimo da mozemo kombinirati 2 stubista u 4x3x2 kvadar. Trivijalno je takvim kvadrima poplocati kocku.