Točno
9. ožujka 2018. 00:41 (8 godine)
Let  be a triangle with circumcircle
be a triangle with circumcircle  and incentre
and incentre  . Let the line passing through
. Let the line passing through  and perpendicular to
and perpendicular to 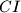 intersect the segment
intersect the segment  and the arc
and the arc  (not containing
(not containing  ) of
) of  at points
at points  and
and  , respectively. Let the line passing through
, respectively. Let the line passing through  and parallel to
and parallel to 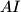 intersect
intersect 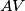 at
at  , and let the line passing through
, and let the line passing through  and parallel to
and parallel to 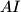 intersect
intersect  at
at  . Let
. Let 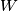 and
and  be the midpoints of
be the midpoints of 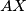 and
and  , respectively. Prove that if the points
, respectively. Prove that if the points  ,
,  , and
, and  are collinear, then the points
are collinear, then the points  ,
, 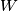 , and
, and  are also collinear.
are also collinear.
(U.S.A.)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Iskoristimo prvo paralelnosti koje su nam dane u zadatku tj. 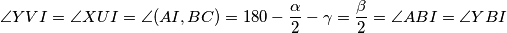
Dakle četverokut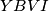 je tetivan, nadalje motivirani ovom tetivnošću definiramo presjek pravaca
je tetivan, nadalje motivirani ovom tetivnošću definiramo presjek pravaca 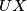 i
i  kao točka
kao točka  . Sada kako je
. Sada kako je 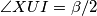 i
i 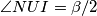 imamo da je
imamo da je 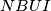 također tetivan. Kratkim angle chaseom ovog kuta dobijamo
također tetivan. Kratkim angle chaseom ovog kuta dobijamo 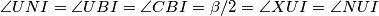 odakle slijedi da je
odakle slijedi da je 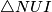 jednakokračan. U ovom trenutku se jos nije razvila neka posebna ideja za rijesiti zadatak pa nastavljamo sa iskorištavanjem uvjeta, tj uvjeta kolinearnosti točaka
jednakokračan. U ovom trenutku se jos nije razvila neka posebna ideja za rijesiti zadatak pa nastavljamo sa iskorištavanjem uvjeta, tj uvjeta kolinearnosti točaka 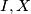 i
i  . Uz paralelnost dobijamo:
. Uz paralelnost dobijamo: 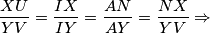
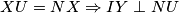 Ili možda u korisnijoj formi
Ili možda u korisnijoj formi 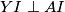 Sada u biti uviđamo neku simetriju sa već definiranom okomicom iz
Sada u biti uviđamo neku simetriju sa već definiranom okomicom iz  na
na 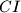 .
.
Problem je kako u skicu na lijep način ubaciti polovišta jer ne izgleda kao da možemo i
i 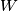 nekako pametno povezati.
nekako pametno povezati.
Sljedeći korak je svakako plodan: definiranje točke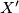 simetričnoj točki
simetričnoj točki  preko
preko  , tu je
, tu je  polovište dužine
polovište dužine 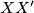 odakle je
odakle je 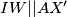 . Sada smo već nekako zgrabili točke
. Sada smo već nekako zgrabili točke 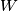 i
i  u neki dio skice, i odmah se možemo lakše igrati... ostaje naravno dokazati
u neki dio skice, i odmah se možemo lakše igrati... ostaje naravno dokazati 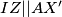 što bi riješilo zadatak.
što bi riješilo zadatak.
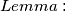
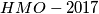 (Arseniy Akopyan EnGeoFigures) prvi dan. Dodajmo polovište
(Arseniy Akopyan EnGeoFigures) prvi dan. Dodajmo polovište  luka
luka  sa točkom
sa točkom  . Lemma glasi da je
. Lemma glasi da je 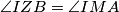
Dokaz lemme ostavljen čitatelju.
Uočimo sličnost trokutova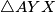 i
i 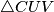 . Trivijalno je
. Trivijalno je 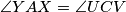 ¸Ne toliko teško dolazimo do jednakosti
¸Ne toliko teško dolazimo do jednakosti 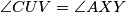 odakle zbog sličnosti slijedi
odakle zbog sličnosti slijedi 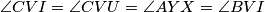 dakle
dakle 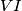 raspolavlja luk
raspolavlja luk  sa
sa  u točki
u točki  . Neka je još
. Neka je još  sjecište
sjecište 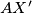 i
i  . Imamo
. Imamo 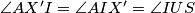 pa
pa 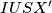 tetivan time je uz
tetivan time je uz 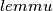 i prije navedeno
i prije navedeno 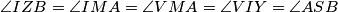 dakle
dakle 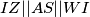 odnosno
odnosno 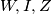 kolinearne
kolinearne
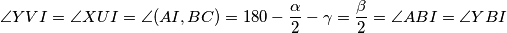
Dakle četverokut
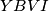 je tetivan, nadalje motivirani ovom tetivnošću definiramo presjek pravaca
je tetivan, nadalje motivirani ovom tetivnošću definiramo presjek pravaca 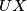 i
i  kao točka
kao točka  . Sada kako je
. Sada kako je 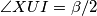 i
i 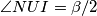 imamo da je
imamo da je 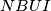 također tetivan. Kratkim angle chaseom ovog kuta dobijamo
također tetivan. Kratkim angle chaseom ovog kuta dobijamo 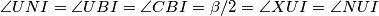 odakle slijedi da je
odakle slijedi da je 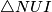 jednakokračan. U ovom trenutku se jos nije razvila neka posebna ideja za rijesiti zadatak pa nastavljamo sa iskorištavanjem uvjeta, tj uvjeta kolinearnosti točaka
jednakokračan. U ovom trenutku se jos nije razvila neka posebna ideja za rijesiti zadatak pa nastavljamo sa iskorištavanjem uvjeta, tj uvjeta kolinearnosti točaka 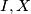 i
i  . Uz paralelnost dobijamo:
. Uz paralelnost dobijamo: 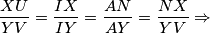
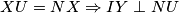 Ili možda u korisnijoj formi
Ili možda u korisnijoj formi 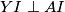 Sada u biti uviđamo neku simetriju sa već definiranom okomicom iz
Sada u biti uviđamo neku simetriju sa već definiranom okomicom iz  na
na 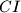 .
.Problem je kako u skicu na lijep način ubaciti polovišta jer ne izgleda kao da možemo
 i
i 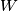 nekako pametno povezati.
nekako pametno povezati.Sljedeći korak je svakako plodan: definiranje točke
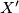 simetričnoj točki
simetričnoj točki  preko
preko  , tu je
, tu je  polovište dužine
polovište dužine 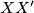 odakle je
odakle je 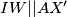 . Sada smo već nekako zgrabili točke
. Sada smo već nekako zgrabili točke 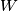 i
i  u neki dio skice, i odmah se možemo lakše igrati... ostaje naravno dokazati
u neki dio skice, i odmah se možemo lakše igrati... ostaje naravno dokazati 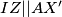 što bi riješilo zadatak.
što bi riješilo zadatak.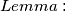
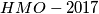 (Arseniy Akopyan EnGeoFigures) prvi dan. Dodajmo polovište
(Arseniy Akopyan EnGeoFigures) prvi dan. Dodajmo polovište  luka
luka  sa točkom
sa točkom  . Lemma glasi da je
. Lemma glasi da je 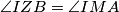
Dokaz lemme ostavljen čitatelju.
Uočimo sličnost trokutova
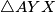 i
i 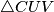 . Trivijalno je
. Trivijalno je 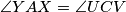 ¸Ne toliko teško dolazimo do jednakosti
¸Ne toliko teško dolazimo do jednakosti 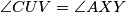 odakle zbog sličnosti slijedi
odakle zbog sličnosti slijedi 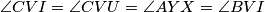 dakle
dakle 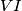 raspolavlja luk
raspolavlja luk  sa
sa  u točki
u točki  . Neka je još
. Neka je još  sjecište
sjecište 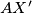 i
i  . Imamo
. Imamo 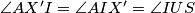 pa
pa 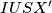 tetivan time je uz
tetivan time je uz 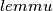 i prije navedeno
i prije navedeno 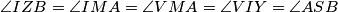 dakle
dakle 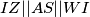 odnosno
odnosno 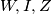 kolinearne
kolinearne  Školjka
Školjka