Točno
13. studenoga 2017. 22:19 (8 godine, 2 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Neka je 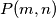 uvrštavanje u izraz
uvrštavanje u izraz 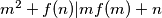
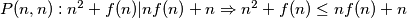 odnosno
odnosno 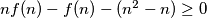 što se lijepše faktorizira u
što se lijepše faktorizira u 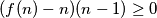
Dakle imamo da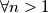 vrijedi
vrijedi 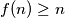
Nadalje nastavljamo sa nasumičnim uvrštavanjem i u jednom trenutku dođemo do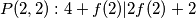 , neka je
, neka je 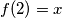 kao i prije vrijedi
kao i prije vrijedi 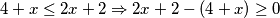
Što koristimo u slijedećem,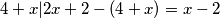 no
no 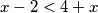 . A za neke prirodne brojeve
. A za neke prirodne brojeve  i
i  takve da je
takve da je 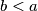 ,
, 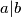 samo ako je
samo ako je 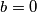 , dakle zaključujemo da
, dakle zaključujemo da 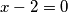 odnosno
odnosno 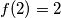 .
.
Kako nekako intuitivno tražimo gornju granicu za , da bi dokazali
, da bi dokazali 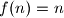 , slijedeći logičan korak je
, slijedeći logičan korak je 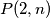 koji daje
koji daje 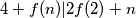 te isto kao i prije dolazimo do
te isto kao i prije dolazimo do 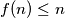
Za imamo
imamo 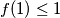 a kako bi funkcija bila definirana za sve prirodne brojeve mora vrijediti
a kako bi funkcija bila definirana za sve prirodne brojeve mora vrijediti 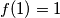 te zaključujemo da je
te zaključujemo da je 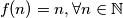
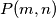 uvrštavanje u izraz
uvrštavanje u izraz 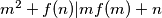
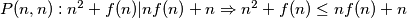 odnosno
odnosno 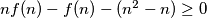 što se lijepše faktorizira u
što se lijepše faktorizira u 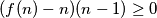
Dakle imamo da
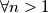 vrijedi
vrijedi 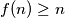
Nadalje nastavljamo sa nasumičnim uvrštavanjem i u jednom trenutku dođemo do
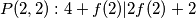 , neka je
, neka je 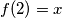 kao i prije vrijedi
kao i prije vrijedi 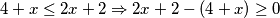
Što koristimo u slijedećem,
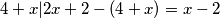 no
no 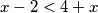 . A za neke prirodne brojeve
. A za neke prirodne brojeve  i
i  takve da je
takve da je 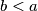 ,
, 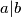 samo ako je
samo ako je 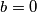 , dakle zaključujemo da
, dakle zaključujemo da 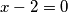 odnosno
odnosno 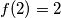 .
.Kako nekako intuitivno tražimo gornju granicu za
 , da bi dokazali
, da bi dokazali 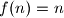 , slijedeći logičan korak je
, slijedeći logičan korak je 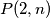 koji daje
koji daje 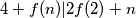 te isto kao i prije dolazimo do
te isto kao i prije dolazimo do 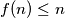
Za
 imamo
imamo 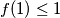 a kako bi funkcija bila definirana za sve prirodne brojeve mora vrijediti
a kako bi funkcija bila definirana za sve prirodne brojeve mora vrijediti 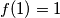 te zaključujemo da je
te zaključujemo da je 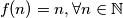
 Školjka
Školjka 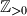 be the set of positive integers. Find all functions
be the set of positive integers. Find all functions 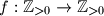 such that
such that 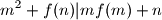 for all positive integers
for all positive integers  and
and  .
.