Točno
14. studenoga 2017. 23:57 (8 godine, 3 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Kako bi pronašli neku donju granicu broja  eksperimentiramo sa vrijednostima
eksperimentiramo sa vrijednostima 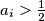 . Za takve
. Za takve  očito vrijedi da je
očito vrijedi da je 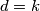 jer u jednu grupu možemo staviti samo ijedan element. Ako posmatramo
jer u jednu grupu možemo staviti samo ijedan element. Ako posmatramo 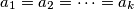 uočavamo da je granični
uočavamo da je granični 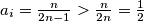 te
te 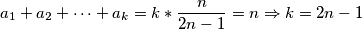 odnosno vrijedi da je
odnosno vrijedi da je 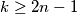 .
.
Sada dodatno strukturiramo zadatak da bi lakše manipulirali vrijednostima. Odnosno definiramo kao minimalni broj grupa
kao minimalni broj grupa 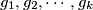 koje su sastavljene od brojeva
koje su sastavljene od brojeva  , strukturu nam daje činjenica da je
, strukturu nam daje činjenica da je 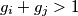 ,
, 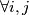 u protivnom bi mogli sastaviti te grupe u jednu što bi bilo kontradiktorno sa minimalnošću broja
u protivnom bi mogli sastaviti te grupe u jednu što bi bilo kontradiktorno sa minimalnošću broja  . Nadalje imamo
. Nadalje imamo 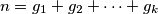
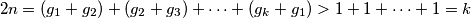
Odakle slijedi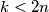 odnosno
odnosno 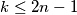 , dakle minimalan broj grupa
, dakle minimalan broj grupa 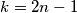 .
.
 eksperimentiramo sa vrijednostima
eksperimentiramo sa vrijednostima 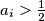 . Za takve
. Za takve  očito vrijedi da je
očito vrijedi da je 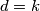 jer u jednu grupu možemo staviti samo ijedan element. Ako posmatramo
jer u jednu grupu možemo staviti samo ijedan element. Ako posmatramo 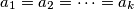 uočavamo da je granični
uočavamo da je granični 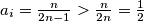 te
te 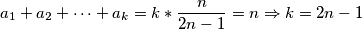 odnosno vrijedi da je
odnosno vrijedi da je 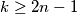 .
.Sada dodatno strukturiramo zadatak da bi lakše manipulirali vrijednostima. Odnosno definiramo
 kao minimalni broj grupa
kao minimalni broj grupa 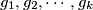 koje su sastavljene od brojeva
koje su sastavljene od brojeva  , strukturu nam daje činjenica da je
, strukturu nam daje činjenica da je 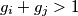 ,
, 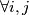 u protivnom bi mogli sastaviti te grupe u jednu što bi bilo kontradiktorno sa minimalnošću broja
u protivnom bi mogli sastaviti te grupe u jednu što bi bilo kontradiktorno sa minimalnošću broja  . Nadalje imamo
. Nadalje imamo 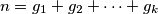
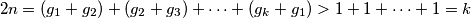
Odakle slijedi
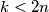 odnosno
odnosno 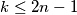 , dakle minimalan broj grupa
, dakle minimalan broj grupa 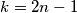 .
.  Školjka
Školjka  be a positive integer. Find the smallest integer
be a positive integer. Find the smallest integer 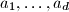 such that
such that 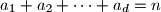 and
and 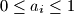 for
for 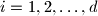 , it is possible to partition these numbers into
, it is possible to partition these numbers into  .
.