Točno
15. studenoga 2017. 02:31 (8 godine, 3 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Prije početka riješavanja dokažimo lemmu koja vrijedi za bilo koji trokut.
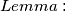 Neka je
Neka je  točka u unutrašnjosti trokuta
točka u unutrašnjosti trokuta  takva da
takva da 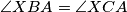 , i neka je
, i neka je  točka takva da je četverokut
točka takva da je četverokut 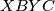 parallelogram. Tada vrijedi
parallelogram. Tada vrijedi 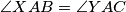
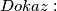 Konstruirajmo točku
Konstruirajmo točku  tako da je četverokut
tako da je četverokut 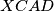 paralelogram tada je
paralelogram tada je 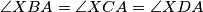 odakle slijedi da je četverokut
odakle slijedi da je četverokut 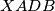 tetivan, uočimo još da je
tetivan, uočimo još da je 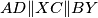 te da je
te da je 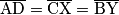 . Dakle iz činjenice da su
. Dakle iz činjenice da su 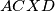 i
i 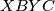 parallelogrami slijedi da je i četverokut
parallelogrami slijedi da je i četverokut 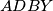 parallelogram. Sada imamo sve što nam je potrebno da dovršimo angle chase.
parallelogram. Sada imamo sve što nam je potrebno da dovršimo angle chase. 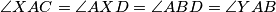
Lemma nam sada ukazuje da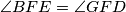 što nam nam hinitira na moguću sličnost nekih trokuta, točnije ako bismo dokazali da
što nam nam hinitira na moguću sličnost nekih trokuta, točnije ako bismo dokazali da 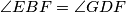 dobili bismo da vrijedi
dobili bismo da vrijedi 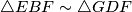 . Sličnost slijedi iz
. Sličnost slijedi iz 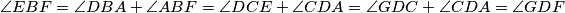
Uz ovo uočavamo da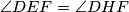 jer je
jer je  preslika točke preko pravca
preslika točke preko pravca 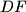
Iz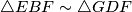 i
i 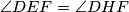 slijedi
slijedi 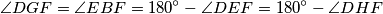
Odakle slijedi da su točke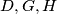 i
i  konciklične.
konciklične. 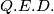
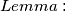 Neka je
Neka je  točka u unutrašnjosti trokuta
točka u unutrašnjosti trokuta  takva da
takva da 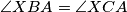 , i neka je
, i neka je  točka takva da je četverokut
točka takva da je četverokut 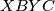 parallelogram. Tada vrijedi
parallelogram. Tada vrijedi 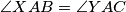
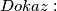 Konstruirajmo točku
Konstruirajmo točku  tako da je četverokut
tako da je četverokut 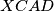 paralelogram tada je
paralelogram tada je 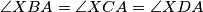 odakle slijedi da je četverokut
odakle slijedi da je četverokut 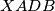 tetivan, uočimo još da je
tetivan, uočimo još da je 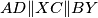 te da je
te da je 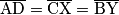 . Dakle iz činjenice da su
. Dakle iz činjenice da su 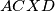 i
i 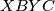 parallelogrami slijedi da je i četverokut
parallelogrami slijedi da je i četverokut 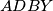 parallelogram. Sada imamo sve što nam je potrebno da dovršimo angle chase.
parallelogram. Sada imamo sve što nam je potrebno da dovršimo angle chase. 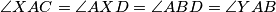
Lemma nam sada ukazuje da
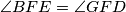 što nam nam hinitira na moguću sličnost nekih trokuta, točnije ako bismo dokazali da
što nam nam hinitira na moguću sličnost nekih trokuta, točnije ako bismo dokazali da 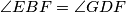 dobili bismo da vrijedi
dobili bismo da vrijedi 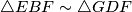 . Sličnost slijedi iz
. Sličnost slijedi iz 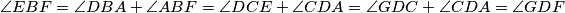
Uz ovo uočavamo da
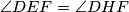 jer je
jer je  preslika točke preko pravca
preslika točke preko pravca 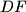
Iz
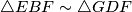 i
i 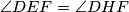 slijedi
slijedi 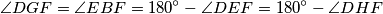
Odakle slijedi da su točke
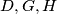 i
i  konciklične.
konciklične. 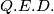
 Školjka
Školjka  be a cyclic quadrilateral whose diagonals
be a cyclic quadrilateral whose diagonals  and
and  meet at
meet at  . The extensions of the sides
. The extensions of the sides  and
and  beyond
beyond  and
and  meet at
meet at  be the point such that
be the point such that 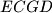 is a parallelogram, and let
is a parallelogram, and let 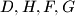 are concyclic.
are concyclic.