Točno
16. studenoga 2017. 02:32 (8 godine, 3 mjeseci)
Call admissible a set

of integers that has the following property:
If
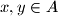
(possibly
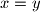
) then
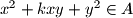
for every integer

.
Determine all pairs
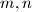
of nonzero integers such that the only admissible set containing both

and

is the set of all integers.
Proposed by Warut Suksompong, Thailand
%V0
Call admissible a set $A$ of integers that has the following property:
If $x,y \in A$ (possibly $x=y$) then $x^2+kxy+y^2 \in A$ for every integer $k$.
Determine all pairs $m,n$ of nonzero integers such that the only admissible set containing both $m$ and $n$ is the set of all integers.
Proposed by Warut Suksompong, Thailand
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Uočimo da ako imamo da je $m \in A $ tada iz uvijeta za $x=y=m$ imamo da je $m^2+kmm+m^2 \in A$ odnosno $ (k+2)m^2 \in A$, lijepše zapisano $$ lm^2\in A, \forall l\in \mathbb{Z}$$
Očito ako vrijedi $gcd(m,n)=1 \Rightarrow gcd(m^2,n^2)=1 $ te $\exists a,b \in \mathbb{Z}$ takvi da $$am^2+bn^2=1$$
Budući da su $m,n \in A$ imamo da su i $am^2,bn^2\in A \Rightarrow (am^2)^2+ 2am^2bn^2+(bn^2)^2 \in A$ odnosno $1=(am^2+bn^2)^2\in A$ te odabirom $x=y=1$ dobijamo $$k+2 \in A, \forall k \in \mathbb{Z}$$ odakle slijedi da je $A\equiv \mathbb{Z}$ za svake $m,n$ takve da je $gcd(m,n)=1$.
Teži dio zadatka je dokazati da za $m,n$ takve da je $gcd(m,n)=d>1$ vrijedi da $A \neq \mathbb{Z}$. Za to pronalazimo eksplicitnu konstrukciju admissible seta. Isprobavanjem dolazimo do zakljucka da je $$A=\{\enspace kd \enspace | \quad \forall k \in \mathbb{Z} \quad \}$$
Uočimo da su $m,n \in A$ te da za svaka dva broja $ad,bd \in A$ imamo da je i $(a^2d+kabd+b^2d)d \in A$. Tako $A$ zadovoljava uvjete admissible seta a ne popunjava skup svih cijelih brojeva.
| 16. studenoga 2017. 14:09 | abeker | Točno |
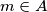 tada iz uvijeta za
tada iz uvijeta za 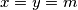 imamo da je
imamo da je 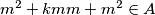 odnosno
odnosno 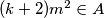 , lijepše zapisano
, lijepše zapisano 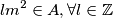 Očito ako vrijedi
Očito ako vrijedi 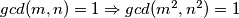 te
te 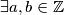 takvi da
takvi da 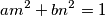 Budući da su
Budući da su 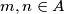 imamo da su i
imamo da su i 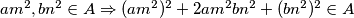 odnosno
odnosno 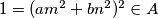 te odabirom
te odabirom 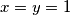 dobijamo
dobijamo 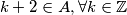 odakle slijedi da je
odakle slijedi da je 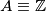 za svake
za svake 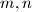 takve da je
takve da je 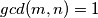 .
.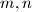 takve da je
takve da je 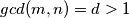 vrijedi da
vrijedi da 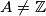 . Za to pronalazimo eksplicitnu konstrukciju admissible seta. Isprobavanjem dolazimo do zakljucka da je
. Za to pronalazimo eksplicitnu konstrukciju admissible seta. Isprobavanjem dolazimo do zakljucka da je  Uočimo da su
Uočimo da su 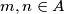 te da za svaka dva broja
te da za svaka dva broja 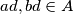 imamo da je i
imamo da je i 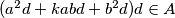 . Tako
. Tako  zadovoljava uvjete admissible seta a ne popunjava skup svih cijelih brojeva.
zadovoljava uvjete admissible seta a ne popunjava skup svih cijelih brojeva.  Školjka
Školjka 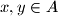 (possibly
(possibly 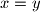 ) then
) then 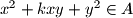 for every integer
for every integer  .
. and
and  is the set of all integers.
is the set of all integers.