Točno
16. studenoga 2017. 14:07 (8 godine, 3 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Riješimo se prvo desne strane nejednakosti, a to je 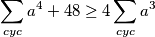
uočimo ovdje da se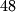 može zapisati u drugom obliku, i to pomoću uvjeta
može zapisati u drugom obliku, i to pomoću uvjeta 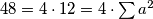
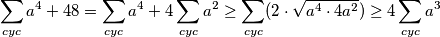
Time je desna strana nejednakosti dokazana, prijeđimo sada na težu stranu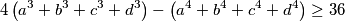
Uočimo da nas izraz podsijeća na neku vrstu kvadratne gdje nam malo taj kub smeta, ali eto pokušajmo
podsijeća na neku vrstu kvadratne gdje nam malo taj kub smeta, ali eto pokušajmo 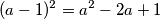 ali tu nema četvrte potencije... Pa kvadrirajmo još jednom!
ali tu nema četvrte potencije... Pa kvadrirajmo još jednom! 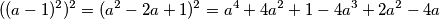 i sve nam se poklapa pojavljuje se član
i sve nam se poklapa pojavljuje se član 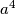 i član
i član 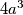 i dijelovi sume sa
i dijelovi sume sa  i
i  , koje znamo dakle gornji ružni izraz možemo zapisati kao
, koje znamo dakle gornji ružni izraz možemo zapisati kao 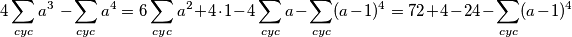 odnosno ostaje dokazati da je
odnosno ostaje dokazati da je
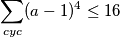
I još jedna stvar koja pomaže u riješavanju zadatka, to jest što nam uvjet hintira je da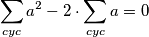
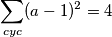
kvadriranjem slijedi
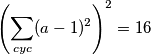
Odnosno malim raspisom imamo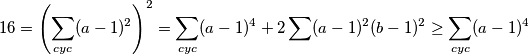
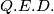
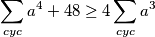
uočimo ovdje da se
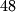 može zapisati u drugom obliku, i to pomoću uvjeta
može zapisati u drugom obliku, i to pomoću uvjeta 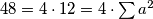
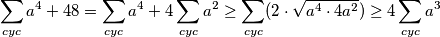
Time je desna strana nejednakosti dokazana, prijeđimo sada na težu stranu
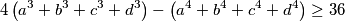
Uočimo da nas izraz
 podsijeća na neku vrstu kvadratne gdje nam malo taj kub smeta, ali eto pokušajmo
podsijeća na neku vrstu kvadratne gdje nam malo taj kub smeta, ali eto pokušajmo 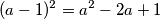 ali tu nema četvrte potencije... Pa kvadrirajmo još jednom!
ali tu nema četvrte potencije... Pa kvadrirajmo još jednom! 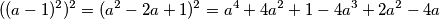 i sve nam se poklapa pojavljuje se član
i sve nam se poklapa pojavljuje se član 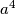 i član
i član 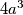 i dijelovi sume sa
i dijelovi sume sa  i
i  , koje znamo dakle gornji ružni izraz možemo zapisati kao
, koje znamo dakle gornji ružni izraz možemo zapisati kao 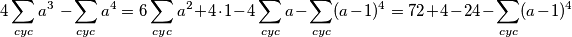 odnosno ostaje dokazati da je
odnosno ostaje dokazati da je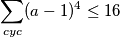
I još jedna stvar koja pomaže u riješavanju zadatka, to jest što nam uvjet hintira je da
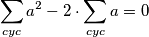
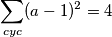
kvadriranjem slijedi
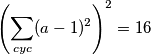
Odnosno malim raspisom imamo
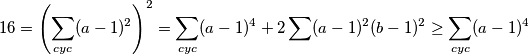
 Školjka
Školjka 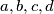 satisfy the relations
satisfy the relations 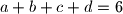 and
and 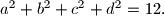 Prove that
Prove that