Točno
23. studenoga 2017. 10:50 (8 godine, 3 mjeseci)
Let  be a triangle with
be a triangle with 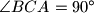 , and let
, and let  be the foot of the altitude from
be the foot of the altitude from  . Let
. Let  be a point in the interior of the segment
be a point in the interior of the segment  . Let
. Let  be the point on the segment
be the point on the segment 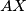 such that
such that 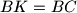 . Similarly, let
. Similarly, let  be the point on the segment
be the point on the segment 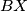 such that
such that 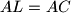 . Let
. Let  be the point of intersection of
be the point of intersection of 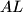 and
and 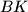 .
.
Show that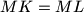 .
.
Proposed by Josef Tkadlec, Czech Republic
 be a triangle with
be a triangle with 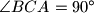 , and let
, and let  be the foot of the altitude from
be the foot of the altitude from  . Let
. Let  be a point in the interior of the segment
be a point in the interior of the segment  . Let
. Let  be the point on the segment
be the point on the segment 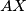 such that
such that 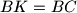 . Similarly, let
. Similarly, let  be the point on the segment
be the point on the segment 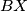 such that
such that 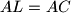 . Let
. Let  be the point of intersection of
be the point of intersection of 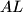 and
and 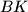 .
.Show that
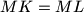 .
.Proposed by Josef Tkadlec, Czech Republic
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Ovaj zadatak iako je G5 ima prilično elementarno riješenje. Kao motivaciju za prvi korak gledamo definiciju točaka  i
i  , odnosno stvaramo način za konstrukciju tih točaka. Definirajmo za tu konstrukciju kružnice
, odnosno stvaramo način za konstrukciju tih točaka. Definirajmo za tu konstrukciju kružnice 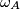 i
i  kao kružnice radijusa
kao kružnice radijusa  i
i  sa centrima u
sa centrima u  i
i  redom. Tada je točka
redom. Tada je točka  jedno od sjecišta kružnice
jedno od sjecišta kružnice 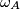 i pravca
i pravca 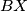 , pa tako definirajmo
, pa tako definirajmo 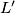 kao drugo sjecište kružnice sa pravcem
kao drugo sjecište kružnice sa pravcem 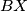 . Slično definiramo
. Slično definiramo  i
i 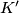 preko
preko  . Definirajmo još jednu točku
. Definirajmo još jednu točku 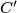 a to je sjecište kružnica
a to je sjecište kružnica 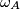 i
i  jer zašto ne ? Tada je
jer zašto ne ? Tada je 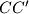 radikalna os
radikalna os 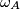 i
i  te vrijedi da je
te vrijedi da je 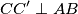
Jer su i
i  centri pripadnih kružnica. Nadalje zaključujemo iz već postavljenog
centri pripadnih kružnica. Nadalje zaključujemo iz već postavljenog 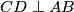 da su točke
da su točke  ,
, ,
, i
i 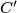 kolinearne. Štoviše jer
kolinearne. Štoviše jer  leži na radikalnoj osi
leži na radikalnoj osi 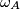 i
i  ima jednaku potenciju na kružnice te vrijedi
ima jednaku potenciju na kružnice te vrijedi 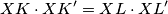
Odakle slijedi da su točke ,
, 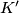 ,
,  i
i 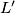 konciklične, nazovimo tu kružnicu
konciklične, nazovimo tu kružnicu  .
.
Sada nam je skica dosta široka i na njoj smo istražili puno generalnih činjenica te smo se time odmakli od tvrdnje zadatka. Pa sa pripremljenim platnom možemo se okomiti na ono što zapravo treba dokazati u zadatku: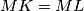
Ako pokušamo pristupiti dokazivanju ove tvrdnje na par klasičnih načina kao dokazati neku jednakost kuteva, ili pronalazak još neke točke koja je jednako udaljena od vidimo da je zadatak imun na takve upade. Jednostavno nam točka
vidimo da je zadatak imun na takve upade. Jednostavno nam točka  ne pruža dovoljno veliku kontrolu nad skicom, i sve činjenice koje smo dobili u zadatku nisu uopće vezane za točku
ne pruža dovoljno veliku kontrolu nad skicom, i sve činjenice koje smo dobili u zadatku nisu uopće vezane za točku  , ta nam opservacija ukazuje da se vrijedi udaljiti od točke
, ta nam opservacija ukazuje da se vrijedi udaljiti od točke  i na neki drugi način probiti zadatak. Tu dolazi u biti pokretač ideje za zadatak
i na neki drugi način probiti zadatak. Tu dolazi u biti pokretač ideje za zadatak  ,
, 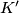 ,
,  i
i 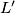 su konciklične točke, i trebamo dokazati da je neka točka jednako udaljena od
su konciklične točke, i trebamo dokazati da je neka točka jednako udaljena od  i
i  na kružnici. Još jednim pogledom na skicu uočavamo da bi
na kružnici. Još jednim pogledom na skicu uočavamo da bi  mogla biti sjecište tangenata iz
mogla biti sjecište tangenata iz  i
i  na
na  .
.
Kao što smo prije rekli, odmaknimo se malo od točke . Odnosno umjesto dokazivanja da je
. Odnosno umjesto dokazivanja da je 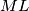 tangentno na
tangentno na  dokazat čemo da je
dokazat čemo da je 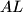 tangentno na
tangentno na  . I sada ulijeće davno zaboravljeni uvijet, koji je prijeko potreban
. I sada ulijeće davno zaboravljeni uvijet, koji je prijeko potreban 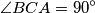
odnosno ako prevedemo u kontekst našeg zadatka sa kružnicama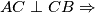
 je tangentno na
je tangentno na  u točki
u točki  pa možemo zaključiti prevođenjem u jezik potencije točke da vrijedi
pa možemo zaključiti prevođenjem u jezik potencije točke da vrijedi 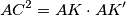 jer
jer  ,
,  ,
, 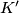 leže na jednom pravcu i
leže na jednom pravcu i  i
i 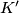 leže na
leže na  . Ali
. Ali  i
i 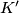 leže i na
leže i na  što nam je upravo i prijelaz sa
što nam je upravo i prijelaz sa  na
na  jer
jer 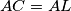 pa
pa 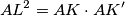 odnosno
odnosno 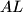 je tangentno na
je tangentno na  , isto tako je
, isto tako je 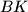 je tangentno na
je tangentno na  odakle slijedi da su
odakle slijedi da su 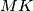 i
i 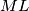 tangentni na
tangentni na  odnosno
odnosno 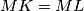 što je i trebalo dokazati.
što je i trebalo dokazati.
 i
i  , odnosno stvaramo način za konstrukciju tih točaka. Definirajmo za tu konstrukciju kružnice
, odnosno stvaramo način za konstrukciju tih točaka. Definirajmo za tu konstrukciju kružnice 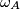 i
i  kao kružnice radijusa
kao kružnice radijusa  i
i  sa centrima u
sa centrima u  i
i  redom. Tada je točka
redom. Tada je točka  jedno od sjecišta kružnice
jedno od sjecišta kružnice 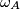 i pravca
i pravca 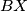 , pa tako definirajmo
, pa tako definirajmo 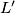 kao drugo sjecište kružnice sa pravcem
kao drugo sjecište kružnice sa pravcem 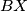 . Slično definiramo
. Slično definiramo  i
i 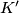 preko
preko  . Definirajmo još jednu točku
. Definirajmo još jednu točku 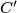 a to je sjecište kružnica
a to je sjecište kružnica 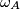 i
i  jer zašto ne ? Tada je
jer zašto ne ? Tada je 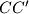 radikalna os
radikalna os 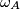 i
i  te vrijedi da je
te vrijedi da je 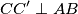
Jer su
 i
i  centri pripadnih kružnica. Nadalje zaključujemo iz već postavljenog
centri pripadnih kružnica. Nadalje zaključujemo iz već postavljenog 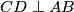 da su točke
da su točke  ,
, ,
, i
i 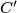 kolinearne. Štoviše jer
kolinearne. Štoviše jer  leži na radikalnoj osi
leži na radikalnoj osi 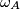 i
i  ima jednaku potenciju na kružnice te vrijedi
ima jednaku potenciju na kružnice te vrijedi 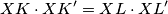
Odakle slijedi da su točke
 ,
, 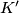 ,
,  i
i 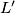 konciklične, nazovimo tu kružnicu
konciklične, nazovimo tu kružnicu  .
.Sada nam je skica dosta široka i na njoj smo istražili puno generalnih činjenica te smo se time odmakli od tvrdnje zadatka. Pa sa pripremljenim platnom možemo se okomiti na ono što zapravo treba dokazati u zadatku:
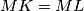
Ako pokušamo pristupiti dokazivanju ove tvrdnje na par klasičnih načina kao dokazati neku jednakost kuteva, ili pronalazak još neke točke koja je jednako udaljena od
 vidimo da je zadatak imun na takve upade. Jednostavno nam točka
vidimo da je zadatak imun na takve upade. Jednostavno nam točka  ne pruža dovoljno veliku kontrolu nad skicom, i sve činjenice koje smo dobili u zadatku nisu uopće vezane za točku
ne pruža dovoljno veliku kontrolu nad skicom, i sve činjenice koje smo dobili u zadatku nisu uopće vezane za točku  , ta nam opservacija ukazuje da se vrijedi udaljiti od točke
, ta nam opservacija ukazuje da se vrijedi udaljiti od točke  i na neki drugi način probiti zadatak. Tu dolazi u biti pokretač ideje za zadatak
i na neki drugi način probiti zadatak. Tu dolazi u biti pokretač ideje za zadatak  ,
, 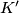 ,
,  i
i 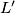 su konciklične točke, i trebamo dokazati da je neka točka jednako udaljena od
su konciklične točke, i trebamo dokazati da je neka točka jednako udaljena od  i
i  na kružnici. Još jednim pogledom na skicu uočavamo da bi
na kružnici. Još jednim pogledom na skicu uočavamo da bi  mogla biti sjecište tangenata iz
mogla biti sjecište tangenata iz  i
i  na
na  .
.Kao što smo prije rekli, odmaknimo se malo od točke
 . Odnosno umjesto dokazivanja da je
. Odnosno umjesto dokazivanja da je 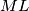 tangentno na
tangentno na  dokazat čemo da je
dokazat čemo da je 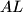 tangentno na
tangentno na  . I sada ulijeće davno zaboravljeni uvijet, koji je prijeko potreban
. I sada ulijeće davno zaboravljeni uvijet, koji je prijeko potreban 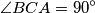
odnosno ako prevedemo u kontekst našeg zadatka sa kružnicama
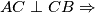
 je tangentno na
je tangentno na  u točki
u točki  pa možemo zaključiti prevođenjem u jezik potencije točke da vrijedi
pa možemo zaključiti prevođenjem u jezik potencije točke da vrijedi 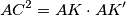 jer
jer  ,
,  ,
, 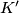 leže na jednom pravcu i
leže na jednom pravcu i  i
i 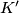 leže na
leže na  . Ali
. Ali  i
i 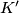 leže i na
leže i na  što nam je upravo i prijelaz sa
što nam je upravo i prijelaz sa  na
na  jer
jer 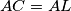 pa
pa 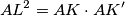 odnosno
odnosno 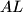 je tangentno na
je tangentno na  , isto tako je
, isto tako je 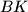 je tangentno na
je tangentno na  odakle slijedi da su
odakle slijedi da su 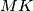 i
i 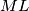 tangentni na
tangentni na  odnosno
odnosno 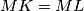 što je i trebalo dokazati.
što je i trebalo dokazati.  Školjka
Školjka