Točno
22. veljače 2018. 01:06 (8 godine)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Prva N5ica :)
Posmatrajmo prvo slučaj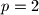 da nas ne zamara tokom rijesavanja, dobijamo
da nas ne zamara tokom rijesavanja, dobijamo 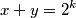 te za neki
te za neki 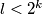 i
i 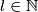 imamo
imamo 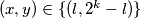
Nadalje pretpostavimo da je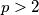 . Neka je
. Neka je 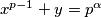 i
i 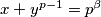 te pretpostavimo
te pretpostavimo 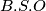 da
da 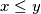 što povlači
što povlači 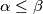 , i
, i 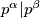 što ćemo kasnije koristiti.
što ćemo kasnije koristiti.
Pokušaji oduzimanja i zbrajanja izraza ne dovode nigdje, barem mene nisu, te pokušavamo direktno s uvrštavanjem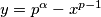 u
u 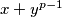 i dobijamo
i dobijamo
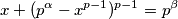
a ovaj korak uistinu i je logičan jer svodimo zadatak na dva bazna broja i
i  .
.
Gledajući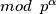 dobijamo :
dobijamo : 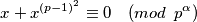
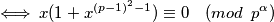 što se grana na dva slučaja
što se grana na dva slučaja 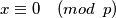 odakle slijedi
odakle slijedi 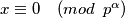 , jer je ova druga zagrada relativno prosta sa
, jer je ova druga zagrada relativno prosta sa  . Tada
. Tada  zapisujemo kao
zapisujemo kao 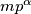 i nizom nejednakosti oblika
i nizom nejednakosti oblika 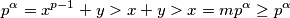 što je očita kontradikcija. Imamo nadalje da je
što je očita kontradikcija. Imamo nadalje da je 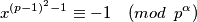 sada se spušamo sa
sada se spušamo sa 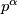 na
na  kako bi primjenili mali fermatov teorem i dobili
kako bi primjenili mali fermatov teorem i dobili 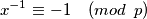
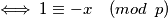
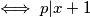
Ideja je poslije ovog spuštanja sa potencije opet se podići i izabrati neki
opet se podići i izabrati neki 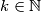 takav da
takav da 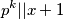
Od prije imamo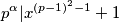
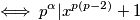
Ovdje je došlo do nekakvog zastoja, jer logično je donekle pokušati nekako uvesti order broja , ta mi je ideja dosta brzo pala u vodu. Nadalje sam pokušao uvesti nekako broj
, ta mi je ideja dosta brzo pala u vodu. Nadalje sam pokušao uvesti nekako broj  i direktna rastava
i direktna rastava 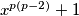 na
na 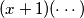 nigdje ne vodi. Tu zastupa prezentacija
nigdje ne vodi. Tu zastupa prezentacija  -a kao
-a kao 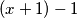 gdje sve odjednom postaje smisleno
gdje sve odjednom postaje smisleno
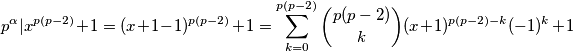
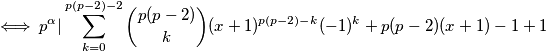 Što čemo zapisati kao
Što čemo zapisati kao 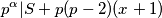 Uočimo da očito
Uočimo da očito 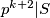 te
te 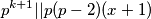 odakle slijedi
odakle slijedi 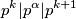 čime smo ograničili
čime smo ograničili  sa
sa 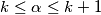
Za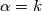 imamo od prije
imamo od prije 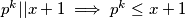 te iz uvjeta
te iz uvjeta 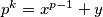 odnosno
odnosno 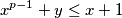 pa su u ovom slučaju
pa su u ovom slučaju  i
i  ijedinice i to ulazi pod slučaj
ijedinice i to ulazi pod slučaj 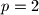 .
.
Za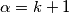 se koristimo sličnom metodom uz malu indukciju
se koristimo sličnom metodom uz malu indukciju 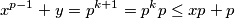 ali za
ali za 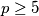 imamo
imamo 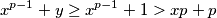 što dokazujemo indukcijom po
što dokazujemo indukcijom po  imajući na umu da je
imajući na umu da je 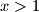 . Za
. Za 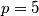 dobijamo
dobijamo 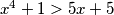 što očito vrijedi
što očito vrijedi
Pretpostavimo da tvrdnja vrijedi za neki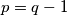 te dokažimo korak
te dokažimo korak 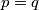
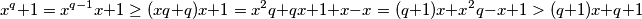
Dakle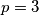 je jedina opcija. Odnosno
je jedina opcija. Odnosno 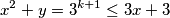 nejednakost se raspada za
nejednakost se raspada za 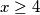 . Za
. Za 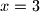 imamo
imamo 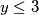 te ubrzo dobijamo da ne postoji takav
te ubrzo dobijamo da ne postoji takav  dok za
dok za 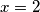 dobijamo riješenje
dobijamo riješenje 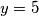 i zaključujemo zadatak navođenjem još dodatna 2 riješenja
i zaključujemo zadatak navođenjem još dodatna 2 riješenja 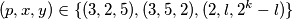
Posmatrajmo prvo slučaj
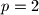 da nas ne zamara tokom rijesavanja, dobijamo
da nas ne zamara tokom rijesavanja, dobijamo 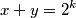 te za neki
te za neki 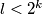 i
i 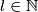 imamo
imamo 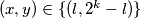
Nadalje pretpostavimo da je
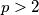 . Neka je
. Neka je 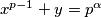 i
i 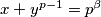 te pretpostavimo
te pretpostavimo 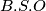 da
da 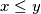 što povlači
što povlači 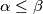 , i
, i 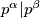 što ćemo kasnije koristiti.
što ćemo kasnije koristiti.Pokušaji oduzimanja i zbrajanja izraza ne dovode nigdje, barem mene nisu, te pokušavamo direktno s uvrštavanjem
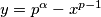 u
u 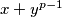 i dobijamo
i dobijamo 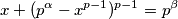
a ovaj korak uistinu i je logičan jer svodimo zadatak na dva bazna broja
 i
i  .
.Gledajući
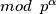 dobijamo :
dobijamo : 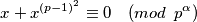
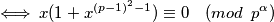 što se grana na dva slučaja
što se grana na dva slučaja 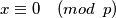 odakle slijedi
odakle slijedi 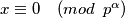 , jer je ova druga zagrada relativno prosta sa
, jer je ova druga zagrada relativno prosta sa  . Tada
. Tada  zapisujemo kao
zapisujemo kao 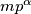 i nizom nejednakosti oblika
i nizom nejednakosti oblika 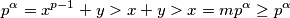 što je očita kontradikcija. Imamo nadalje da je
što je očita kontradikcija. Imamo nadalje da je 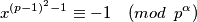 sada se spušamo sa
sada se spušamo sa 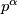 na
na  kako bi primjenili mali fermatov teorem i dobili
kako bi primjenili mali fermatov teorem i dobili 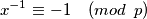
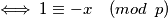
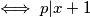
Ideja je poslije ovog spuštanja sa potencije
 opet se podići i izabrati neki
opet se podići i izabrati neki 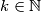 takav da
takav da 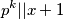
Od prije imamo
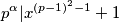
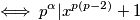
Ovdje je došlo do nekakvog zastoja, jer logično je donekle pokušati nekako uvesti order broja
 , ta mi je ideja dosta brzo pala u vodu. Nadalje sam pokušao uvesti nekako broj
, ta mi je ideja dosta brzo pala u vodu. Nadalje sam pokušao uvesti nekako broj  i direktna rastava
i direktna rastava 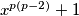 na
na 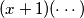 nigdje ne vodi. Tu zastupa prezentacija
nigdje ne vodi. Tu zastupa prezentacija  -a kao
-a kao 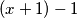 gdje sve odjednom postaje smisleno
gdje sve odjednom postaje smisleno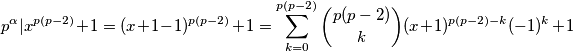
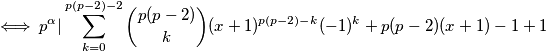 Što čemo zapisati kao
Što čemo zapisati kao 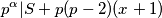 Uočimo da očito
Uočimo da očito 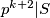 te
te 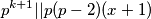 odakle slijedi
odakle slijedi 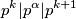 čime smo ograničili
čime smo ograničili  sa
sa 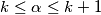
Za
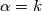 imamo od prije
imamo od prije 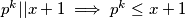 te iz uvjeta
te iz uvjeta 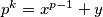 odnosno
odnosno 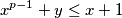 pa su u ovom slučaju
pa su u ovom slučaju  i
i  ijedinice i to ulazi pod slučaj
ijedinice i to ulazi pod slučaj 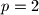 .
.Za
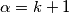 se koristimo sličnom metodom uz malu indukciju
se koristimo sličnom metodom uz malu indukciju 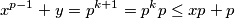 ali za
ali za 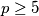 imamo
imamo 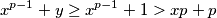 što dokazujemo indukcijom po
što dokazujemo indukcijom po  imajući na umu da je
imajući na umu da je 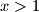 . Za
. Za 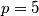 dobijamo
dobijamo 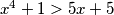 što očito vrijedi
što očito vrijediPretpostavimo da tvrdnja vrijedi za neki
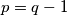 te dokažimo korak
te dokažimo korak 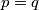
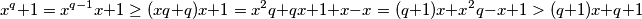
Dakle
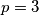 je jedina opcija. Odnosno
je jedina opcija. Odnosno 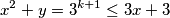 nejednakost se raspada za
nejednakost se raspada za 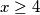 . Za
. Za 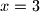 imamo
imamo 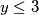 te ubrzo dobijamo da ne postoji takav
te ubrzo dobijamo da ne postoji takav  dok za
dok za 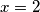 dobijamo riješenje
dobijamo riješenje 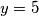 i zaključujemo zadatak navođenjem još dodatna 2 riješenja
i zaključujemo zadatak navođenjem još dodatna 2 riješenja 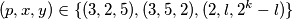
 Školjka
Školjka 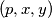 consisting of a prime number
consisting of a prime number 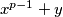 and
and 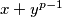 are both powers of
are both powers of