Točno
8. prosinca 2017. 23:54 (8 godine, 3 mjeseci)
If

are three positive real numbers such that
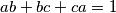
, prove that
![\sqrt[3]{ \frac{1}{a} + 6b} + \sqrt[3]{\frac{1}{b} + 6c} + \sqrt[3]{\frac{1}{c} + 6a } \leq \frac{1}{abc}.](/media/m/b/8/1/b8152e5174c814f5f157b14f7eb88b60.png)
%V0
If $a, b, c$ are three positive real numbers such that $ab+bc+ca = 1$, prove that $$\sqrt[3]{ \frac{1}{a} + 6b} + \sqrt[3]{\frac{1}{b} + 6c} + \sqrt[3]{\frac{1}{c} + 6a } \leq \frac{1}{abc}.$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Promatrajmo funkciju
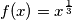
odakle proizlazi
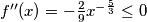
dakle možemo po Jensenovj nejednakosti zaključiti da vrijedi
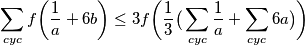
dakle ostaje nam dokazati da je
![\sqrt[3]{9\frac{1}{abc} +54\sum_{cyc}a}\leq \frac{1}{abc}](/media/m/b/7/4/b748190c63d0543461f0428bf380a615.png)
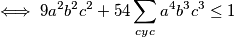
Što dovršavama vrlo jednostavno sa dvije nejednakosti
![3\sqrt[3]{a^2b^2c^2} \leq ab+bc+ca =1 \implies a^2b^2c^2\leq\frac{1}{27}](/media/m/6/e/2/6e2b32b454cd22c308348efa4f1585fe.png)
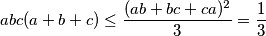
Dakle
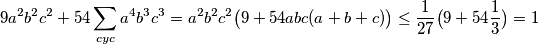
%V0 Promatrajmo funkciju $f(x)=x^{\frac{1}{3}}$ odakle proizlazi $f''(x)=-\frac{2}{9}x^{-\frac{5}{3}}\leq 0$ dakle možemo po Jensenovj nejednakosti zaključiti da vrijedi
$$\sum_{cyc} f\bigg(\frac{1}{a}+6b\bigg) \leq 3 f\bigg(\frac{1}{3}\big(\sum_{cyc} \frac{1}{a} + \sum_{cyc} 6a \big)\bigg)$$ dakle ostaje nam dokazati da je $$\sqrt[3]{9\frac{1}{abc} +54\sum_{cyc}a}\leq \frac{1}{abc}$$ $$\iff 9a^2b^2c^2 +54\sum_{cyc}a^4b^3c^3\leq 1$$
Što dovršavama vrlo jednostavno sa dvije nejednakosti $$ 3\sqrt[3]{a^2b^2c^2} \leq ab+bc+ca =1 \implies a^2b^2c^2\leq\frac{1}{27}$$
$$abc(a+b+c)\leq\frac{(ab+bc+ca)^2}{3}=\frac{1}{3}$$
Dakle $$9a^2b^2c^2 +54\sum_{cyc}a^4b^3c^3=a^2b^2c^2 \big( 9 + 54 abc ( a + b+ c) \big) \leq \frac{1}{27}\big( 9 +54 \frac{1}{3}\big)=1$$
| 10. prosinca 2017. 01:59 | Lugo | Točno |