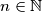Točno
18. travnja 2012. 18:09 (13 godine, 10 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
BSOMP 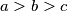 a kako su svi elementi N i
a kako su svi elementi N i 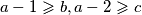
Dakle sigurno vrijedi
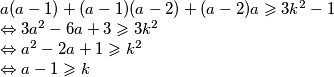
Pokažimo da tada zadatak sigurno vrijedi za tri uzastopna broja
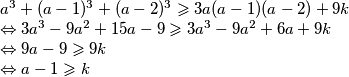
Što smo dokazali da slijedi iz uvjeta zadatka
Dakle, za svaka tri uzastopna broja ovo vrijedi. Sada pretpostavimo da postoje neki i
i takvi da
takvi da 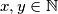
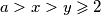
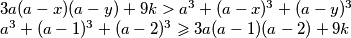
Zbrajanjem ovih nejednakosti dobivamo
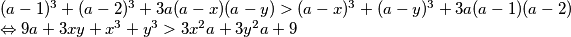
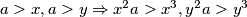
Pa imamo
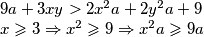
Pa dobivamo
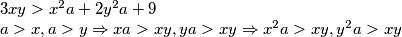
Pa imamo
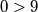
što je kontrdadikcija. Dakle, ne postoje prirodni brojevi brojevi manji od takvi da
takvi da
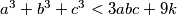
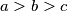 a kako su svi elementi N i
a kako su svi elementi N i 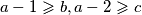
Dakle sigurno vrijedi
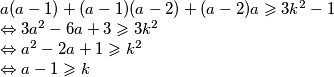
Pokažimo da tada zadatak sigurno vrijedi za tri uzastopna broja
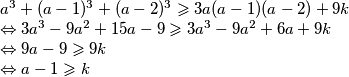
Što smo dokazali da slijedi iz uvjeta zadatka
Dakle, za svaka tri uzastopna broja ovo vrijedi. Sada pretpostavimo da postoje neki
 i
i takvi da
takvi da 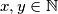
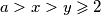
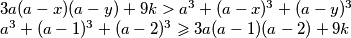
Zbrajanjem ovih nejednakosti dobivamo
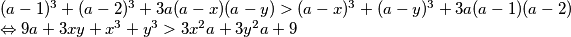
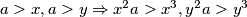
Pa imamo
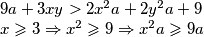
Pa dobivamo
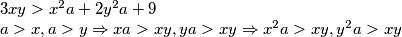
Pa imamo
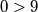
što je kontrdadikcija. Dakle, ne postoje prirodni brojevi brojevi manji od
 takvi da
takvi da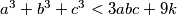
Ocjene: (1)
Komentari:
Veki, 19. travnja 2012. 22:22
ikicic, 19. travnja 2012. 19:44
kokan, 19. travnja 2012. 14:58
mimaro, 19. travnja 2012. 14:55
Ovo je krivo (koliko se meni čini).
Stavivši tamo dolje a-1 umjesto b i a-2 umjesto c; maksimiziraš lijevu stranu nejdnakosti po varijablama a,b,c (doduše i desnu isto), a to ne smiješ.
Naime, pokažeš da je Max(Lijevo)>=Max(desno) za neki fiksni a. Ali to nije dovoljno. Jer znaš samo Max(Lijevo)>=Lijevo i Max(Desno)>=Desno, i Max(Lijevo)>=Max(desno). A iz toga ne možeš zaključiti Lijevo>=Desno.
Jesam li u krivu?
Stavivši tamo dolje a-1 umjesto b i a-2 umjesto c; maksimiziraš lijevu stranu nejdnakosti po varijablama a,b,c (doduše i desnu isto), a to ne smiješ.
Naime, pokažeš da je Max(Lijevo)>=Max(desno) za neki fiksni a. Ali to nije dovoljno. Jer znaš samo Max(Lijevo)>=Lijevo i Max(Desno)>=Desno, i Max(Lijevo)>=Max(desno). A iz toga ne možeš zaključiti Lijevo>=Desno.
Jesam li u krivu?
 Školjka
Školjka  ,
,  različiti prirodni brojevi i
različiti prirodni brojevi i  prirodan broj takav da vrijedi
prirodan broj takav da vrijedi 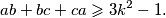
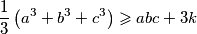 .
.