Točno
18. travnja 2012. 18:09 (13 godine, 10 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Za svaka dva međusobno jednaka realna broja jednakost očito vrijedi. Vrijedi i ako je jedan od brojeva  , a drugi proizvoljan realan broj. Vrijedi i za svaka dva cjela broja jer
, a drugi proizvoljan realan broj. Vrijedi i za svaka dva cjela broja jer 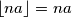 za sve cjelobrojne
za sve cjelobrojne  i
i  .
.
Definirajmo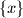 kao decimalni dio od
kao decimalni dio od  to jest
to jest 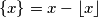 .
.
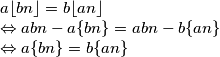
Pretpostavimo da su i
i  različiti racionalni brojevi, s različitim nazivnicima.
različiti racionalni brojevi, s različitim nazivnicima.
Tada postoji takav da
takav da 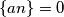 , a
, a 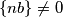 , ili naopako. Dakle očito su nazivnici jednaki.
, ili naopako. Dakle očito su nazivnici jednaki.
Označimo taj nazivnik s , a brojnike s
, a brojnike s  i
i  . Ako je
. Ako je 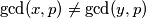 onda ponovo mozemo naci
onda ponovo mozemo naci  takav da je jedna strana jednakosti
takav da je jedna strana jednakosti  a druga nije.
a druga nije.
BSOMP
Neka je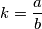
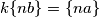
Kako je racionalan,
racionalan, 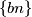 će imati konačno mnogo vrijednosti koje će se periodički ponavljati za različite
će imati konačno mnogo vrijednosti koje će se periodički ponavljati za različite  .
.
Uzmimo najveću od tih vrjednosti. Neka se ona postiže za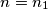 .
.
 to postižu iste ostatke znamo iz činjenoce da
to postižu iste ostatke znamo iz činjenoce da 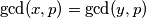
Kako je, zbog pretpostavke, slijedi
slijedi 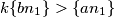
Dakle, jednakost ne vrijedi, pa dva racionalna broja (različita od nula) i međusobno različita ne zadovoljavaju uvjete zadatka.
Pretpostavimo sada da da su i i
i  iracionalni.
iracionalni.
BSOMP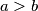
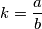
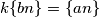
Iz dirichletovog principa znamo da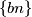 može biti proizvoljno blizu
može biti proizvoljno blizu  , pa sigurno
, pa sigurno 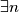 takav da
takav da 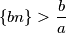 pa je za taj
pa je za taj 
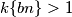 , a
, a 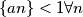
Pa jednoakost ne može vrijediti.
Ako je racionalan, a
racionalan, a  nije, postoji n takav da
nije, postoji n takav da 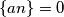 , što za
, što za  ne postoji.
ne postoji.
Dakle jedina rje[enja su:
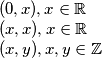
 , a drugi proizvoljan realan broj. Vrijedi i za svaka dva cjela broja jer
, a drugi proizvoljan realan broj. Vrijedi i za svaka dva cjela broja jer 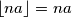 za sve cjelobrojne
za sve cjelobrojne  i
i  .
.Definirajmo
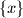 kao decimalni dio od
kao decimalni dio od  to jest
to jest 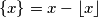 .
.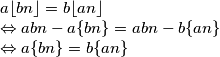
Pretpostavimo da su
 i
i  različiti racionalni brojevi, s različitim nazivnicima.
različiti racionalni brojevi, s različitim nazivnicima.Tada postoji
 takav da
takav da 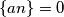 , a
, a 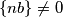 , ili naopako. Dakle očito su nazivnici jednaki.
, ili naopako. Dakle očito su nazivnici jednaki.Označimo taj nazivnik s
 , a brojnike s
, a brojnike s  i
i  . Ako je
. Ako je 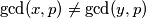 onda ponovo mozemo naci
onda ponovo mozemo naci  takav da je jedna strana jednakosti
takav da je jedna strana jednakosti  a druga nije.
a druga nije.BSOMP
Neka je
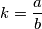
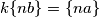
Kako je
 racionalan,
racionalan, 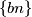 će imati konačno mnogo vrijednosti koje će se periodički ponavljati za različite
će imati konačno mnogo vrijednosti koje će se periodički ponavljati za različite  .
.Uzmimo najveću od tih vrjednosti. Neka se ona postiže za
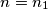 .
. to postižu iste ostatke znamo iz činjenoce da
to postižu iste ostatke znamo iz činjenoce da 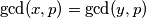
Kako je, zbog pretpostavke,
 slijedi
slijedi 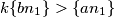
Dakle, jednakost ne vrijedi, pa dva racionalna broja (različita od nula) i međusobno različita ne zadovoljavaju uvjete zadatka.
Pretpostavimo sada da da su i
 i
i  iracionalni.
iracionalni.BSOMP
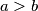
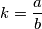
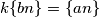
Iz dirichletovog principa znamo da
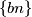 može biti proizvoljno blizu
može biti proizvoljno blizu  , pa sigurno
, pa sigurno 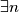 takav da
takav da 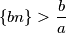 pa je za taj
pa je za taj 
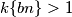 , a
, a 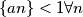
Pa jednoakost ne može vrijediti.
Ako je
 racionalan, a
racionalan, a  nije, postoji n takav da
nije, postoji n takav da 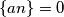 , što za
, što za  ne postoji.
ne postoji.Dakle jedina rje[enja su:
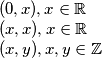
 Školjka
Školjka 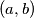 of real numbers such that
of real numbers such that 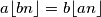 for all positive integers
for all positive integers 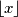 denotes the greatest integer less than or equal to
denotes the greatest integer less than or equal to