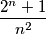Neocijenjeno
16. ožujka 2018. 08:22 (7 godine, 12 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Uvjet zadatka je ekvivalentan sa 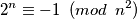
Neka je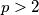 najmanji prosti djelitelj broja
najmanji prosti djelitelj broja  . Broj
. Broj  nije
nije  jer tada ne dijeli
jer tada ne dijeli 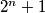
Vrijedi
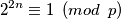
Odnosno kako vrijedi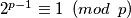 imamo i
imamo i 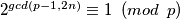 . Kako
. Kako 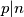 i
i  je najmanji takav slijedi da
je najmanji takav slijedi da 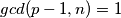 pa zatim
pa zatim 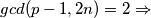
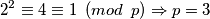
Odnosno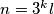 za neki
za neki 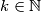 tj. sada vrijedi
tj. sada vrijedi 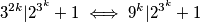
Posmatrajmo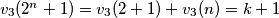 ali s druge strane je
ali s druge strane je 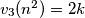 dakle
dakle 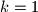 odnosno
odnosno 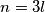
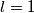 nas dovodi do rijesenja
nas dovodi do rijesenja 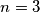
Pretpostavimo tada da i neka je
i neka je 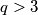 najmanji prosti djelitelj od
najmanji prosti djelitelj od  .
.
Tada imamo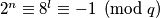 odnosno
odnosno 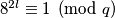 što uz
što uz 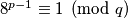 daje
daje 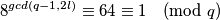 dakle
dakle 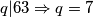
Ali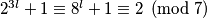 što vodi u kontradikciju jer s druge strane
što vodi u kontradikciju jer s druge strane 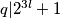 Dakle takav
Dakle takav  ne postoji i jedino rijesenje je
ne postoji i jedino rijesenje je 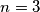
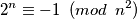
Neka je
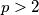 najmanji prosti djelitelj broja
najmanji prosti djelitelj broja  . Broj
. Broj  nije
nije  jer tada ne dijeli
jer tada ne dijeli 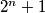
Vrijedi
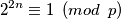
Odnosno kako vrijedi
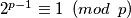 imamo i
imamo i 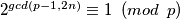 . Kako
. Kako 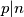 i
i  je najmanji takav slijedi da
je najmanji takav slijedi da 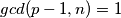 pa zatim
pa zatim 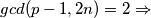
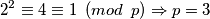
Odnosno
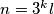 za neki
za neki 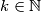 tj. sada vrijedi
tj. sada vrijedi 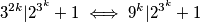
Posmatrajmo
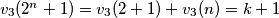 ali s druge strane je
ali s druge strane je 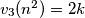 dakle
dakle 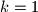 odnosno
odnosno 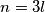
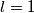 nas dovodi do rijesenja
nas dovodi do rijesenja 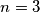
Pretpostavimo tada da
 i neka je
i neka je 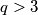 najmanji prosti djelitelj od
najmanji prosti djelitelj od  .
.Tada imamo
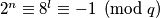 odnosno
odnosno 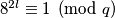 što uz
što uz 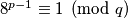 daje
daje 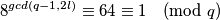 dakle
dakle 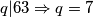
Ali
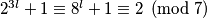 što vodi u kontradikciju jer s druge strane
što vodi u kontradikciju jer s druge strane 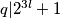 Dakle takav
Dakle takav  ne postoji i jedino rijesenje je
ne postoji i jedino rijesenje je 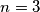
 Školjka
Školjka 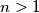 such that
such that