Kliknite ovdje kako biste prikazali rješenje.
Neka su točke 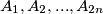 vrhovi pravilnog 2n-terokuta. Znamo da dani 2n-terokut možemo prikazati u kompleksnoj ravnini tako što svaki vrh
vrhovi pravilnog 2n-terokuta. Znamo da dani 2n-terokut možemo prikazati u kompleksnoj ravnini tako što svaki vrh 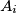 označimo s kompleksnim brojem
označimo s kompleksnim brojem 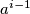 gdje je
gdje je 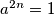 . Neka je u permutaciji vrh
. Neka je u permutaciji vrh 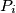 označen s
označen s 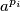 gdje je
gdje je 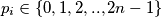
Uvjet da bi neke dvije dužine  i
i 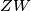 bile paralelne u kompleksnoj ravnini je
bile paralelne u kompleksnoj ravnini je 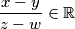 , odnosno,
, odnosno, 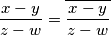 . Promotrimo što bi trebalo vrijediti za neke
. Promotrimo što bi trebalo vrijediti za neke 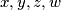 da bi
da bi 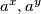 i
i 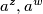 bile paralelne dužine.
bile paralelne dužine.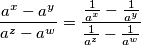 gdje smo iskoristili da je
gdje smo iskoristili da je 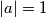 . Sređivanjem izraza dobivamo da je
. Sređivanjem izraza dobivamo da je 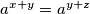 odakle slijedi da je
odakle slijedi da je 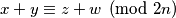 .
.
Dokažimo sada da u svakoj permutaciji postoje dva para uzastopnih brojeva kojima je suma jedana modulo 2n. Pretpostavimo da postoji permutacija u kojoj takvi brojevi ne postoje. S obzirom da imamo ukupno 2n uzastopnih parova, oni predstavljaju brojeve 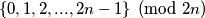 . Ako promotrimo sumu svih tih parova, ona je jednaka
. Ako promotrimo sumu svih tih parova, ona je jednaka 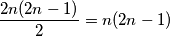 što očito nije djeljivo s 2n. Ako promotrimo tu sumu kao dvostruku sumu svih parova brojeva, uočavamo da je ta suma jednaka
što očito nije djeljivo s 2n. Ako promotrimo tu sumu kao dvostruku sumu svih parova brojeva, uočavamo da je ta suma jednaka 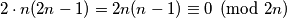 odakle slijedi kontradikcija te naša početna pretpostavka da takva permutacija ne postoji je netočna. Time je dokazano da uvijek možemo naći 2 para brojeva
odakle slijedi kontradikcija te naša početna pretpostavka da takva permutacija ne postoji je netočna. Time je dokazano da uvijek možemo naći 2 para brojeva 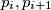 i
i 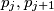 tako da oni predstavljaju paralelne dužine što smo i trebali dokazati.
tako da oni predstavljaju paralelne dužine što smo i trebali dokazati.
 Školjka
Školjka 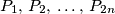 permutacija vrhova pravilnog
permutacija vrhova pravilnog  -terokuta. Dokaži da zatvorena poligonalna linija koja se sastoji od dužina
-terokuta. Dokaži da zatvorena poligonalna linija koja se sastoji od dužina 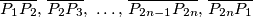 sadrži barem jedan par paralelnih dužina.
sadrži barem jedan par paralelnih dužina.