Točno
13. ožujka 2018. 22:02 (7 godine, 12 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Prvo izaberemo prvih 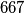 članova kao
članova kao  sljedećih toliko sa
sljedećih toliko sa 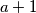 i zadnjih
i zadnjih 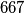 sa
sa 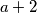 , ovom konstrukcijom uviđamo da je
, ovom konstrukcijom uviđamo da je 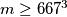
Uočimo da su u tročlanom podskupu svi elementi različiti modulo to nas motivira da posmatramo neki skup
to nas motivira da posmatramo neki skup  sa
sa  brojeva kongruentni
brojeva kongruentni  modulo
modulo  ,
,  brojeva kongruentni
brojeva kongruentni  modulo
modulo  i
i  brojeva kongruentno
brojeva kongruentno  . Uočimo da vrijedi slijedeća tvrdnja
. Uočimo da vrijedi slijedeća tvrdnja
 podskupova
podskupova 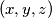 gdje su
gdje su 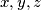 u parovima različti
u parovima različti 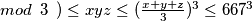
Kombiniranjem konstrukcije i gornje ograde na zaključujemo da
zaključujemo da 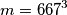
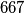 članova kao
članova kao  sljedećih toliko sa
sljedećih toliko sa 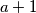 i zadnjih
i zadnjih 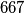 sa
sa 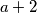 , ovom konstrukcijom uviđamo da je
, ovom konstrukcijom uviđamo da je 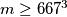
Uočimo da su u tročlanom podskupu svi elementi različiti modulo
 to nas motivira da posmatramo neki skup
to nas motivira da posmatramo neki skup  sa
sa  brojeva kongruentni
brojeva kongruentni  modulo
modulo  ,
,  brojeva kongruentni
brojeva kongruentni  modulo
modulo  i
i  brojeva kongruentno
brojeva kongruentno  . Uočimo da vrijedi slijedeća tvrdnja
. Uočimo da vrijedi slijedeća tvrdnja podskupova
podskupova 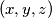 gdje su
gdje su 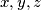 u parovima različti
u parovima različti 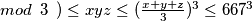
Kombiniranjem konstrukcije i gornje ograde na
 zaključujemo da
zaključujemo da 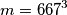
 Školjka
Školjka 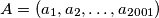 be a sequence of positive integers. Let
be a sequence of positive integers. Let 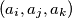 with
with 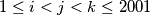 , such that
, such that 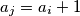 and
and 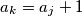 . Considering all such sequences
. Considering all such sequences