Točno
13. ožujka 2018. 21:47 (7 godine, 11 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Neka je 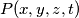 uvrštavanje u
uvrštavanje u 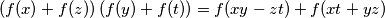 za svake realne
za svake realne 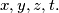
Sa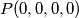 dobivamo
dobivamo 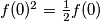 i dva moguća rijesenja za
i dva moguća rijesenja za 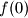
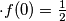 odakle sa
odakle sa 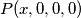 dobijamo
dobijamo 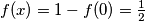 za svaki
za svaki 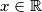
I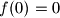 što možemo pretpostaviti nadalje do kraja rijesenja
što možemo pretpostaviti nadalje do kraja rijesenja
Iskorištavamo simetriju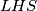 i proveravamo
i proveravamo 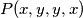 što nas plodno nagrađuje sa svojstvom
što nas plodno nagrađuje sa svojstvom 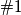
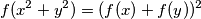
Istražujući simetriju na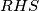 poigravamo se sa čudno zadanim uvijetom i kako bi se u potpunosti riješili drugog clana biramo
poigravamo se sa čudno zadanim uvijetom i kako bi se u potpunosti riješili drugog clana biramo 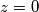 pa
pa
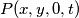 daje
daje 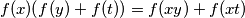 gdje nas uvrštavanje
gdje nas uvrštavanje 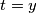 dovodi do svojstva
dovodi do svojstva 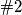
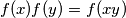
Odnosno još bitnije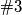
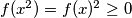
Ako umjesto prijašnjeg ne učinimo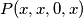 nego
nego 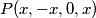 dobijamo
dobijamo 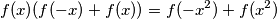
Ako kvadriramo i iskoristimo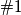 imamo
imamo 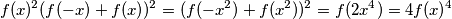
gdje je zadnji korak bio primjena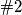 , nadalje dobijamo da je
, nadalje dobijamo da je
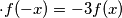 odakle iz
odakle iz 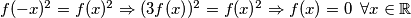
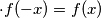 čime ćemo se voditi do kraja riješenja
čime ćemo se voditi do kraja riješenja
Parnost u paru sa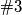 daje
daje 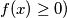
Stavljajući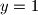 u multiplikativnost dobijamo
u multiplikativnost dobijamo 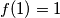 , naoružani jedinicom uvrštavamo
, naoružani jedinicom uvrštavamo 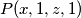 kako bismo iskoristili najvise iz umnozaka na
kako bismo iskoristili najvise iz umnozaka na 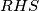
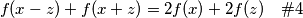
Dokažimo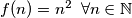 indukcijom
indukcijom
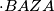
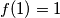 što smo već otprije dokazali
što smo već otprije dokazali
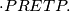
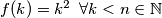
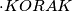
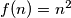
 koristimo se sa
koristimo se sa 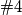 u obliku
u obliku 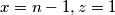 da dobijemo
da dobijemo 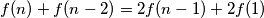
 što korištenjem pretpostavke prelazi u
što korištenjem pretpostavke prelazi u 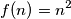
...
Zaključujemo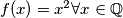
...
Zatim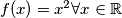 provjeravanjem slučajeva
provjeravanjem slučajeva 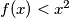 i
i 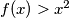
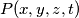 uvrštavanje u
uvrštavanje u 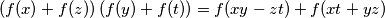 za svake realne
za svake realne 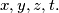
Sa
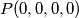 dobivamo
dobivamo 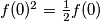 i dva moguća rijesenja za
i dva moguća rijesenja za 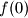
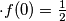 odakle sa
odakle sa 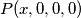 dobijamo
dobijamo 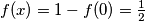 za svaki
za svaki 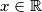
I
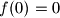 što možemo pretpostaviti nadalje do kraja rijesenja
što možemo pretpostaviti nadalje do kraja rijesenjaIskorištavamo simetriju
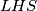 i proveravamo
i proveravamo 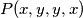 što nas plodno nagrađuje sa svojstvom
što nas plodno nagrađuje sa svojstvom 
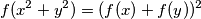
Istražujući simetriju na
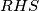 poigravamo se sa čudno zadanim uvijetom i kako bi se u potpunosti riješili drugog clana biramo
poigravamo se sa čudno zadanim uvijetom i kako bi se u potpunosti riješili drugog clana biramo 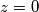 pa
pa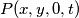 daje
daje 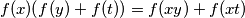 gdje nas uvrštavanje
gdje nas uvrštavanje 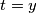 dovodi do svojstva
dovodi do svojstva 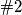
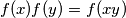
Odnosno još bitnije
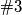
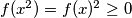
Ako umjesto prijašnjeg ne učinimo
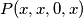 nego
nego 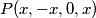 dobijamo
dobijamo 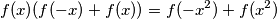
Ako kvadriramo i iskoristimo
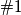 imamo
imamo 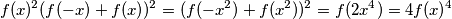
gdje je zadnji korak bio primjena
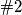 , nadalje dobijamo da je
, nadalje dobijamo da je 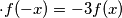 odakle iz
odakle iz 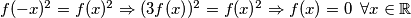
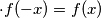 čime ćemo se voditi do kraja riješenja
čime ćemo se voditi do kraja riješenjaParnost u paru sa
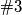 daje
daje 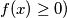
Stavljajući
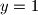 u multiplikativnost dobijamo
u multiplikativnost dobijamo 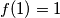 , naoružani jedinicom uvrštavamo
, naoružani jedinicom uvrštavamo 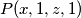 kako bismo iskoristili najvise iz umnozaka na
kako bismo iskoristili najvise iz umnozaka na 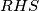
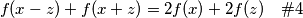
Dokažimo
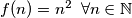 indukcijom
indukcijom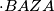
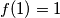 što smo već otprije dokazali
što smo već otprije dokazali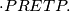
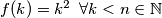
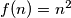
 koristimo se sa
koristimo se sa 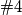 u obliku
u obliku 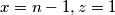 da dobijemo
da dobijemo 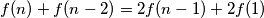
 što korištenjem pretpostavke prelazi u
što korištenjem pretpostavke prelazi u 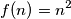
...
Zaključujemo
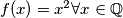
...
Zatim
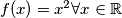 provjeravanjem slučajeva
provjeravanjem slučajeva 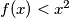 i
i 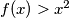
 Školjka
Školjka  from the reals to the reals such that
from the reals to the reals such that 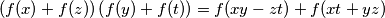 for all real
for all real 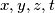 .
.