Točno
18. ožujka 2018. 22:47 (7 godine, 10 mjeseci)
Dokažite da za svaka tri realna broja

,

,

vrijedi nejednakost
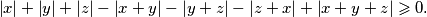
%V0
Dokažite da za svaka tri realna broja $x$, $y$, $z$ vrijedi nejednakost $$\left\vert x \right\vert + \left\vert y \right\vert + \left\vert z \right\vert - \left\vert x+y \right\vert - \left\vert y+z \right\vert - \left\vert z+x \right\vert + \left\vert x+y+z \right\vert \geqslant 0 \text{.}$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
$f(x) = |x|$ je konveksna funkcija, pa po Popoviciu nejednakosti slijedi:
$$|x|+|y|+|z| + 3\Big|\frac{x+y+z}{3}\Big| \geqslant 2\Bigg(\Big|\frac{x+y}{2}\Big|+ \Big|\frac{y+z}{2}\Big|+\Big|\frac{z+x}{2}\Big|\Bigg)$$
$Q.E.D.$