Točno
24. ožujka 2018. 20:39 (7 godine, 11 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Neka je 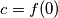 i
i 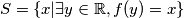 . Pretpostavimo da je
. Pretpostavimo da je 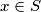 i
i 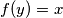 . Tada uvrštavanjem
. Tada uvrštavanjem  u
u  slijedi
slijedi
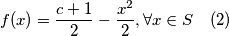
Uvrštavanjem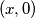 u
u  dobivamo da je
dobivamo da je
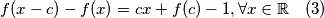
Pretpostavimo da je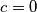 . Kako je
. Kako je 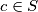 je
je 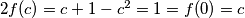 što je kontradikcija. Dakle
što je kontradikcija. Dakle 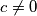 . Stoga je funkcija
. Stoga je funkcija 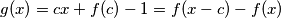 surjekcija pa to
surjekcija pa to 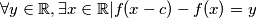 odnosno
odnosno 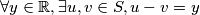 .
.
No tada je zbog i
i 
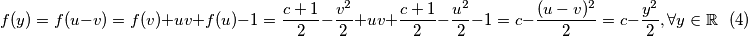
Posebice ako u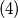 vrijedi
vrijedi 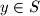 zbog
zbog  vrijedi
vrijedi 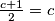 odnosno
odnosno 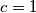 .
.
Iz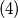 dobivamo da
dobivamo da
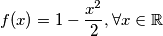
što se uvrštavanjem potvrđuje kao rješenje.
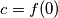 i
i 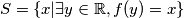 . Pretpostavimo da je
. Pretpostavimo da je 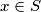 i
i 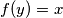 . Tada uvrštavanjem
. Tada uvrštavanjem  u
u  slijedi
slijedi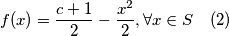
Uvrštavanjem
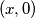 u
u  dobivamo da je
dobivamo da je 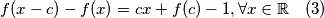
Pretpostavimo da je
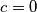 . Kako je
. Kako je 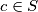 je
je 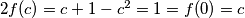 što je kontradikcija. Dakle
što je kontradikcija. Dakle 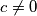 . Stoga je funkcija
. Stoga je funkcija 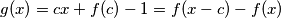 surjekcija pa to
surjekcija pa to 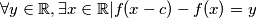 odnosno
odnosno 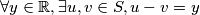 .
.No tada je zbog
 i
i 
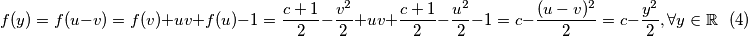
Posebice ako u
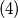 vrijedi
vrijedi 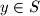 zbog
zbog  vrijedi
vrijedi 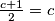 odnosno
odnosno 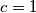 .
.Iz
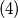 dobivamo da
dobivamo da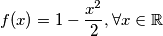
što se uvrštavanjem potvrđuje kao rješenje.
 Školjka
Školjka  such that
such that 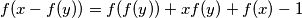
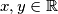 .
.