Neocijenjeno
1. travnja 2018. 00:29 (7 godine, 11 mjeseci)
In Happy City there are 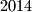 citizens called
citizens called 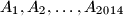 . Each of them is either happy or unhappy at any moment in time. The mood of any citizen
. Each of them is either happy or unhappy at any moment in time. The mood of any citizen  changes (from being unhappy to being happy or vice versa) if and only if some other happy citizen smiles at
changes (from being unhappy to being happy or vice versa) if and only if some other happy citizen smiles at  . On Monday morning there were
. On Monday morning there were  happy citizens in the city.
happy citizens in the city.
The following happened on Monday during the day: citizen smiled at citizen
smiled at citizen 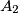 , then
, then 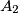 smiled at
smiled at 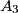 , etc., and, finally,
, etc., and, finally, 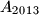 smiled at
smiled at 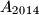 . Nobody smiled at anyone else apart from this. Exactly the same repeated on Tuesday, Wednesday and Thursday. There were exactly
. Nobody smiled at anyone else apart from this. Exactly the same repeated on Tuesday, Wednesday and Thursday. There were exactly 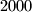 happy citizens on Thursday evening.
happy citizens on Thursday evening.
Determine the largest possible value of .
.
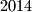 citizens called
citizens called 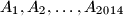 . Each of them is either happy or unhappy at any moment in time. The mood of any citizen
. Each of them is either happy or unhappy at any moment in time. The mood of any citizen  changes (from being unhappy to being happy or vice versa) if and only if some other happy citizen smiles at
changes (from being unhappy to being happy or vice versa) if and only if some other happy citizen smiles at  . On Monday morning there were
. On Monday morning there were  happy citizens in the city.
happy citizens in the city.The following happened on Monday during the day: citizen
 smiled at citizen
smiled at citizen 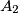 , then
, then 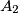 smiled at
smiled at 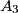 , etc., and, finally,
, etc., and, finally, 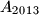 smiled at
smiled at 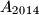 . Nobody smiled at anyone else apart from this. Exactly the same repeated on Tuesday, Wednesday and Thursday. There were exactly
. Nobody smiled at anyone else apart from this. Exactly the same repeated on Tuesday, Wednesday and Thursday. There were exactly 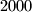 happy citizens on Thursday evening.
happy citizens on Thursday evening.Determine the largest possible value of
 .
. Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Neka je 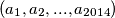 konfiguracija raspoloženja građana prije bilo koje interakcije spomenute u zadatku. Pritom je
konfiguracija raspoloženja građana prije bilo koje interakcije spomenute u zadatku. Pritom je  raspoloženje osobe
raspoloženje osobe 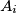 s tim da je
s tim da je 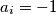 ako je
ako je 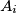 sretan, a
sretan, a 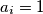 ako je
ako je 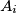 nesretan. Neka je
nesretan. Neka je 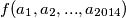 konfiguracija raspoloženja nakon što se svaki
konfiguracija raspoloženja nakon što se svaki 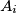 nasmije
nasmije 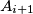 , a da je
, a da je 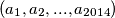 prijašnja konfiguracija. Iteraciju funkcije
prijašnja konfiguracija. Iteraciju funkcije 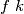 puta na konfiguraciju
puta na konfiguraciju 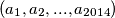 označavamo s
označavamo s 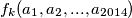 . Po prirodi promjene raspoloženja kakva je opisana u zadatku vrijedi
. Po prirodi promjene raspoloženja kakva je opisana u zadatku vrijedi 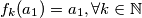 . Nadalje imamo
. Nadalje imamo 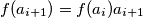 te šire
te šire 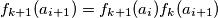 . Poznato nam je i
. Poznato nam je i 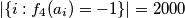 .
.
Promotrimo prvih nekoliko vrijednosti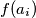 . Slijedimo li tvrdnje gore lako dobijemo
. Slijedimo li tvrdnje gore lako dobijemo 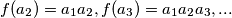 . Dade se naslutiti i induktivno dokazati da je
. Dade se naslutiti i induktivno dokazati da je
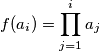
Daljnjim ružnim raspisivanjem se opet dade naslutiti i induktivno dokazati sljedeće
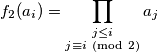
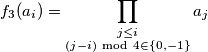
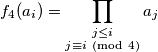
Sada po ostatku pri dijeljenju s konfiguraciju
konfiguraciju 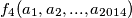 možemo podijeliti na 4 po faktorima disjunktne potkonfiguracije,
možemo podijeliti na 4 po faktorima disjunktne potkonfiguracije, 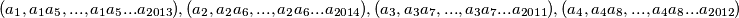 . Uočimo da na svake dvije
. Uočimo da na svake dvije  dolazi barem jedna
dolazi barem jedna  te da ako je neki početni član
te da ako je neki početni član  , na tu barem jednu
, na tu barem jednu  dolazi maksimalno jedna
dolazi maksimalno jedna  . Stoga je optimalno ako na svaku od 14
. Stoga je optimalno ako na svaku od 14  dolaze dvije
dolaze dvije  te ako su svi početni članovi
te ako su svi početni članovi  . Zaključujemo da je
. Zaključujemo da je 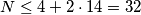 .
.
Za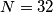 nudimo sada jasan primjer. Neka je
nudimo sada jasan primjer. Neka je 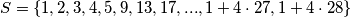 . Ako je
. Ako je 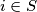 tada neka je
tada neka je 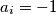 , a u suprotnom
, a u suprotnom 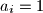 .
.
Stoga je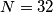 doista najveći mogući broj sretnih građana.
doista najveći mogući broj sretnih građana.
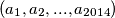 konfiguracija raspoloženja građana prije bilo koje interakcije spomenute u zadatku. Pritom je
konfiguracija raspoloženja građana prije bilo koje interakcije spomenute u zadatku. Pritom je  raspoloženje osobe
raspoloženje osobe 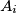 s tim da je
s tim da je 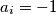 ako je
ako je 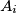 sretan, a
sretan, a 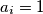 ako je
ako je 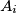 nesretan. Neka je
nesretan. Neka je 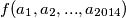 konfiguracija raspoloženja nakon što se svaki
konfiguracija raspoloženja nakon što se svaki 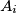 nasmije
nasmije 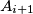 , a da je
, a da je 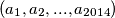 prijašnja konfiguracija. Iteraciju funkcije
prijašnja konfiguracija. Iteraciju funkcije 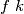 puta na konfiguraciju
puta na konfiguraciju 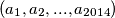 označavamo s
označavamo s 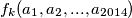 . Po prirodi promjene raspoloženja kakva je opisana u zadatku vrijedi
. Po prirodi promjene raspoloženja kakva je opisana u zadatku vrijedi 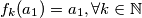 . Nadalje imamo
. Nadalje imamo 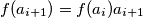 te šire
te šire 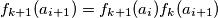 . Poznato nam je i
. Poznato nam je i 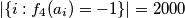 .
.Promotrimo prvih nekoliko vrijednosti
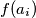 . Slijedimo li tvrdnje gore lako dobijemo
. Slijedimo li tvrdnje gore lako dobijemo 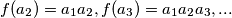 . Dade se naslutiti i induktivno dokazati da je
. Dade se naslutiti i induktivno dokazati da je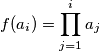
Daljnjim ružnim raspisivanjem se opet dade naslutiti i induktivno dokazati sljedeće
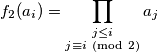
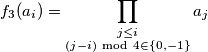
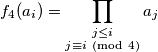
Sada po ostatku pri dijeljenju s
 konfiguraciju
konfiguraciju 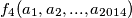 možemo podijeliti na 4 po faktorima disjunktne potkonfiguracije,
možemo podijeliti na 4 po faktorima disjunktne potkonfiguracije,  . Uočimo da na svake dvije
. Uočimo da na svake dvije  dolazi barem jedna
dolazi barem jedna  te da ako je neki početni član
te da ako je neki početni član  , na tu barem jednu
, na tu barem jednu  dolazi maksimalno jedna
dolazi maksimalno jedna  . Stoga je optimalno ako na svaku od 14
. Stoga je optimalno ako na svaku od 14  dolaze dvije
dolaze dvije  te ako su svi početni članovi
te ako su svi početni članovi  . Zaključujemo da je
. Zaključujemo da je  .
.Za
 nudimo sada jasan primjer. Neka je
nudimo sada jasan primjer. Neka je  . Ako je
. Ako je 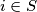 tada neka je
tada neka je 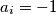 , a u suprotnom
, a u suprotnom 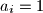 .
.Stoga je
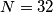 doista najveći mogući broj sretnih građana.
doista najveći mogući broj sretnih građana.  Školjka
Školjka