Točno
5. travnja 2018. 16:20 (6 godine, 8 mjeseci)
Prove that the fraction
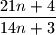
is irreducible for every natural number
.
%V0
Prove that the fraction $\dfrac{21n + 4}{14n + 3}$ is irreducible for every natural number $n$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Pretpostavimo da se dani razlomak može skratiti.Onda vrijedi D(21n+4,14n+3)>1.Kako je po euklidovom algoritmu: D(21n+4,14n+3)=D(14n+3,(21n+4-(14n+3))=D(14n+3,7n+1), slijedi D(14n+3,7n+1)=D(14n+3,14n+2)=1,te dobivamo: D(21n+4,14n+3)=1,odnosno,dani razlomak se ne može skratiti.
Pretpostavimo da se dani razlomak može skratiti.Onda vrijedi D(21n+4,14n+3)>1.Kako je po euklidovom algoritmu:
D(21n+4,14n+3)=D(14n+3,(21n+4-(14n+3))=D(14n+3,7n+1),
slijedi D(14n+3,7n+1)=D(14n+3,14n+2)=1,te dobivamo:
D(21n+4,14n+3)=1,odnosno,dani razlomak se ne može skratiti.
Školjka