Neocijenjeno
9. travnja 2018. 01:31 (7 godine, 11 mjeseci)
A rectangle  is partitioned in several (
is partitioned in several (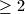 ) rectangles with sides parallel to those of
) rectangles with sides parallel to those of  . Given that any line parallel to one of the sides of
. Given that any line parallel to one of the sides of  , and having common points with the interior of
, and having common points with the interior of  , also has common interior points with the interior of at least one rectangle of the partition; prove that there is at least one rectangle of the partition having no common points with
, also has common interior points with the interior of at least one rectangle of the partition; prove that there is at least one rectangle of the partition having no common points with  's boundary.
's boundary.
Author: unknown author, Japan
 is partitioned in several (
is partitioned in several (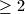 ) rectangles with sides parallel to those of
) rectangles with sides parallel to those of  . Given that any line parallel to one of the sides of
. Given that any line parallel to one of the sides of  , and having common points with the interior of
, and having common points with the interior of  , also has common interior points with the interior of at least one rectangle of the partition; prove that there is at least one rectangle of the partition having no common points with
, also has common interior points with the interior of at least one rectangle of the partition; prove that there is at least one rectangle of the partition having no common points with  's boundary.
's boundary. Author: unknown author, Japan
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Pretpostavimo suprotno, tj. da svi pravokutnici sadrže točku na rubu pravokutnika  . Po principu ekstrema postoji minimalna particija pravokutnika
. Po principu ekstrema postoji minimalna particija pravokutnika  na
na  dijelova.
dijelova.
Označimo donji lijevi vrh od sa
sa  i neka je
i neka je 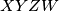 pravokutnik koji sadrzi točku
pravokutnik koji sadrzi točku  tako da je
tako da je  u unutrašnjosti
u unutrašnjosti  .
.
Nazovimo točku dobrom ako leži na stranici nekog pravokutnika u patriciji pravokutnika .
.
Kako je obložen pravokutnicima mora postojati dobra točka na produžecima barem jedne od stranica
obložen pravokutnicima mora postojati dobra točka na produžecima barem jedne od stranica 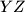 i
i 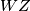 . Neka je B.S.O. to pravac
. Neka je B.S.O. to pravac 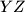 i neka je
i neka je  točka na produžetku
točka na produžetku 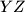 takva da je udaljenost od
takva da je udaljenost od  do
do  maksimalna. Istom logikom postoji i dobra točka
maksimalna. Istom logikom postoji i dobra točka  tako da su
tako da su  i
i  s iste strane pravca
s iste strane pravca 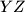 i
i 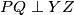 , odaberimo
, odaberimo  tako da je udaljenost
tako da je udaljenost  minimalna. Ako bi se
minimalna. Ako bi se  nalazila na pravcu
nalazila na pravcu 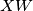 tada bi pravokutnike
tada bi pravokutnike 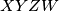 i
i 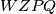 mogli posmatrati zajedno i
mogli posmatrati zajedno i 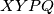 bi bio validan pravokutnik za popločavanje pravokutnika
bi bio validan pravokutnik za popločavanje pravokutnika  što bi bilo kontradiktorno s minimalnošću broja
što bi bilo kontradiktorno s minimalnošću broja  .
.
Time postoji pravokutnik sa vrhom koji se nalazi na duži
koji se nalazi na duži 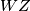 i naravno točka
i naravno točka  koja pripada tom pravokutniku t.d.
koja pripada tom pravokutniku t.d. 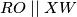
Za kraj nam ostaje samo promatrati prostor ograđen pravcima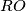 ,
, 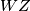 ,
, 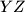 i
i  koji je odvojen od ruba pravokutnika
koji je odvojen od ruba pravokutnika  odnosno
odnosno 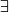 pravokutnik
pravokutnik  u ograđenom prostoru t.d.
u ograđenom prostoru t.d.  ne dijeli zajedničke točke sa
ne dijeli zajedničke točke sa  . Ovaj nas zaključak dovodi do kontradikcije sa početnom pretpostavkom te vrijedi da postoji barem jedan pravokutnik u particiji pravokutnika
. Ovaj nas zaključak dovodi do kontradikcije sa početnom pretpostavkom te vrijedi da postoji barem jedan pravokutnik u particiji pravokutnika  koji ne dijeli zajedničke točke sa
koji ne dijeli zajedničke točke sa 

 . Po principu ekstrema postoji minimalna particija pravokutnika
. Po principu ekstrema postoji minimalna particija pravokutnika  na
na  dijelova.
dijelova.Označimo donji lijevi vrh od
 sa
sa  i neka je
i neka je 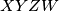 pravokutnik koji sadrzi točku
pravokutnik koji sadrzi točku  tako da je
tako da je  u unutrašnjosti
u unutrašnjosti  .
.Nazovimo točku dobrom ako leži na stranici nekog pravokutnika u patriciji pravokutnika
 .
. Kako je
 obložen pravokutnicima mora postojati dobra točka na produžecima barem jedne od stranica
obložen pravokutnicima mora postojati dobra točka na produžecima barem jedne od stranica 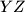 i
i 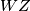 . Neka je B.S.O. to pravac
. Neka je B.S.O. to pravac 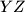 i neka je
i neka je  točka na produžetku
točka na produžetku 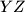 takva da je udaljenost od
takva da je udaljenost od  do
do  maksimalna. Istom logikom postoji i dobra točka
maksimalna. Istom logikom postoji i dobra točka  tako da su
tako da su  i
i  s iste strane pravca
s iste strane pravca 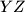 i
i 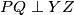 , odaberimo
, odaberimo  tako da je udaljenost
tako da je udaljenost  minimalna. Ako bi se
minimalna. Ako bi se  nalazila na pravcu
nalazila na pravcu 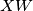 tada bi pravokutnike
tada bi pravokutnike 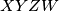 i
i 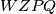 mogli posmatrati zajedno i
mogli posmatrati zajedno i 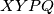 bi bio validan pravokutnik za popločavanje pravokutnika
bi bio validan pravokutnik za popločavanje pravokutnika  što bi bilo kontradiktorno s minimalnošću broja
što bi bilo kontradiktorno s minimalnošću broja  .
. Time postoji pravokutnik sa vrhom
 koji se nalazi na duži
koji se nalazi na duži 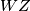 i naravno točka
i naravno točka  koja pripada tom pravokutniku t.d.
koja pripada tom pravokutniku t.d. 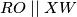
Za kraj nam ostaje samo promatrati prostor ograđen pravcima
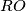 ,
, 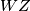 ,
, 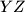 i
i  koji je odvojen od ruba pravokutnika
koji je odvojen od ruba pravokutnika  odnosno
odnosno 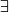 pravokutnik
pravokutnik  u ograđenom prostoru t.d.
u ograđenom prostoru t.d.  ne dijeli zajedničke točke sa
ne dijeli zajedničke točke sa  . Ovaj nas zaključak dovodi do kontradikcije sa početnom pretpostavkom te vrijedi da postoji barem jedan pravokutnik u particiji pravokutnika
. Ovaj nas zaključak dovodi do kontradikcije sa početnom pretpostavkom te vrijedi da postoji barem jedan pravokutnik u particiji pravokutnika  koji ne dijeli zajedničke točke sa
koji ne dijeli zajedničke točke sa 

 Školjka
Školjka