Let
 be a nonnegative integer.
be a nonnegative integer.A forest consists of rooted (i. e. oriented) trees. Each vertex of the forest is either a leaf or has two successors. A vertex
 is called an extended successor of a vertex
is called an extended successor of a vertex  if there is a chain of vertices
if there is a chain of vertices 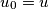 ,
, 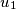 ,
, 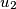 , ...,
, ..., 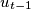 ,
, 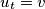 with
with 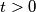 such that the vertex
such that the vertex 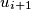 is a successor of the vertex
is a successor of the vertex 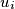 for every integer
for every integer  with
with 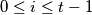 . A vertex is called dynastic if it has two successors and each of these successors has at least
. A vertex is called dynastic if it has two successors and each of these successors has at least  extended successors.
extended successors.Prove that if the forest has
 vertices, then there are at most
vertices, then there are at most 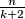 dynastic vertices.
dynastic vertices. Kliknite ovdje kako biste prikazali rješenje.
Označimo sa  broj dinastičkih čvorova u šumi. Svakom dinastičkom čvoru
broj dinastičkih čvorova u šumi. Svakom dinastičkom čvoru  pridružimo skup sebe i njegovih potomaka
pridružimo skup sebe i njegovih potomaka 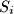 . (Potomak je extended succesor) Također, svakom dinastičkom čvoru pridružimo skup
. (Potomak je extended succesor) Također, svakom dinastičkom čvoru pridružimo skup 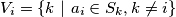 . Za svaki čvor koji ima djecu, odaberimo lijevo i desno dijete tog čvora.
. Za svaki čvor koji ima djecu, odaberimo lijevo i desno dijete tog čvora.
Na stablu vršimo sljedeći algoritam:
Dok postoji, odaberimo dinastički čvor  takav da
takav da 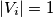 (takav očito postoji ako nisu svi
(takav očito postoji ako nisu svi 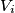 prazni). Neka
prazni). Neka 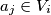 . Iz skupa
. Iz skupa 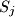 uklonimo
uklonimo  , njegovo lijevo dijete i sve potomke tog djeteta, a iz skupa
, njegovo lijevo dijete i sve potomke tog djeteta, a iz skupa 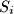 desno dijete
desno dijete  i sve potomke tog djeteta. "Osvježimo" skupove
i sve potomke tog djeteta. "Osvježimo" skupove 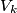 za sve
za sve  . Nakon ovoga, vrijedi
. Nakon ovoga, vrijedi 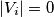 i
i 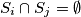 Također, primijetimo da
Također, primijetimo da 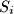 sadrži
sadrži  , njegovo lijevo dijete i potomke tog djeteta (njih barem
, njegovo lijevo dijete i potomke tog djeteta (njih barem  ) pa
) pa 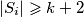 . Analogno,
. Analogno, 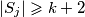 .
.
Algoritam očito terminira (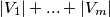 se smanjuje) te nakon njegovog izvođenja su skupovi
se smanjuje) te nakon njegovog izvođenja su skupovi 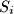 disjunktni i vrijedi
disjunktni i vrijedi 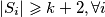 .
.
Prema tome 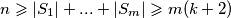 pa
pa 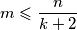 , što je i trebalo pokazati.
, što je i trebalo pokazati.
 Školjka
Školjka