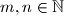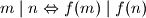Točno
9. veljače 2013. 17:52 (12 godine, 11 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Iz surjektivnosti znamo da postoji  takav da
takav da 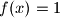 .
.
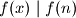
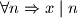
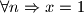
Pokazimo prvo injektivnost.
Pretpostavimo da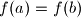
Kako tada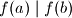 i
i 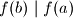 vrijedi i
vrijedi i 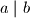 i
i 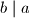 . Dakle
. Dakle 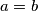
Broj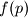 mora imati tocno 2 djeljitelja (jedan od kojih je 1) za svaki prost broj
mora imati tocno 2 djeljitelja (jedan od kojih je 1) za svaki prost broj  . Dakle
. Dakle 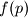 je prost.
je prost.
Pretpostavimo da vrijedi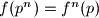 (baza indukcije ce biti
(baza indukcije ce biti  )
)
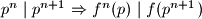
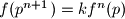
Iz uvjeta zadatka znamo da je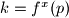
Ako je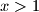 tada postoji broj
tada postoji broj 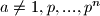 takav da
takav da 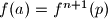 pa ocito
pa ocito 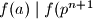 ali
ali  ne dijeli
ne dijeli 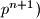 kontradikcija!
kontradikcija!
Dakle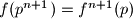
Pokazimo jos i da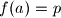 ,
,  prost implicira
prost implicira  prost. (potrebno je samo pogledati broj djeljitelja brojeva
prost. (potrebno je samo pogledati broj djeljitelja brojeva  i
i  )
)
Sada pronadimo formulu za sve prirodne brojeve
Ako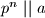 onda
onda 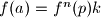 uz
uz 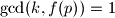
Kako to vrijedi za svaki takav da
takav da 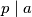 , dobivamo da je
, dobivamo da je 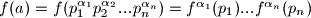
Dakle, sada jos samo preostaje definirati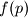 za sve proste
za sve proste  . Lagano provjerom dobiva se da za svaku bijektivnu funkciju
. Lagano provjerom dobiva se da za svaku bijektivnu funkciju 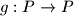 (gdje je skup
(gdje je skup  skup prostih brojeva) i
skup prostih brojeva) i 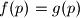 za sve proste
za sve proste  zadatak vrijedi.
zadatak vrijedi.
 takav da
takav da 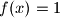 .
.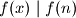
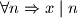
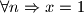
Pokazimo prvo injektivnost.
Pretpostavimo da
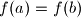
Kako tada
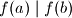 i
i 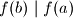 vrijedi i
vrijedi i 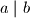 i
i 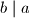 . Dakle
. Dakle 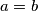
Broj
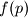 mora imati tocno 2 djeljitelja (jedan od kojih je 1) za svaki prost broj
mora imati tocno 2 djeljitelja (jedan od kojih je 1) za svaki prost broj  . Dakle
. Dakle 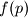 je prost.
je prost.Pretpostavimo da vrijedi
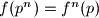 (baza indukcije ce biti
(baza indukcije ce biti  )
)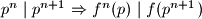
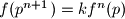
Iz uvjeta zadatka znamo da je
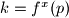
Ako je
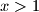 tada postoji broj
tada postoji broj 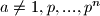 takav da
takav da 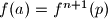 pa ocito
pa ocito 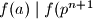 ali
ali  ne dijeli
ne dijeli 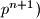 kontradikcija!
kontradikcija!Dakle
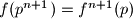
Pokazimo jos i da
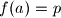 ,
,  prost implicira
prost implicira  prost. (potrebno je samo pogledati broj djeljitelja brojeva
prost. (potrebno je samo pogledati broj djeljitelja brojeva  i
i  )
)Sada pronadimo formulu za sve prirodne brojeve
Ako
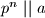 onda
onda 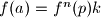 uz
uz 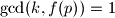
Kako to vrijedi za svaki
 takav da
takav da 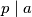 , dobivamo da je
, dobivamo da je 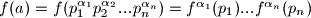
Dakle, sada jos samo preostaje definirati
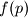 za sve proste
za sve proste  . Lagano provjerom dobiva se da za svaku bijektivnu funkciju
. Lagano provjerom dobiva se da za svaku bijektivnu funkciju 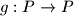 (gdje je skup
(gdje je skup  skup prostih brojeva) i
skup prostih brojeva) i 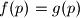 za sve proste
za sve proste  zadatak vrijedi.
zadatak vrijedi.  Školjka
Školjka 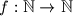 such that for all
such that for all