Neocijenjeno
15. srpnja 2018. 04:54 (7 godine, 8 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Neka je  presjek kružnica
presjek kružnica 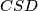 i
i 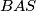 . Kako je
. Kako je  radikalno središte kružnica
radikalno središte kružnica  ,
, 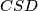 , i
, i 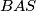 , mora se nalaziti na radikalnoj osi kružnica
, mora se nalaziti na radikalnoj osi kružnica 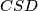 i
i 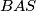 što je pravac
što je pravac 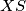 , odnosno,
, odnosno,  ,
,  i
i  su kolinearne. Uočimo da je
su kolinearne. Uočimo da je 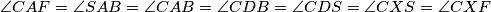 (sve tvrdnje slijede iz kolinearnosti nekih točaka ili tetivnosti nekih četverokuta), odnosno, četverokut
(sve tvrdnje slijede iz kolinearnosti nekih točaka ili tetivnosti nekih četverokuta), odnosno, četverokut 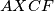 je tetivan pa je
je tetivan pa je 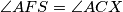 .
.
Definirajmo 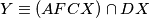 i
i 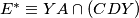 . Uočimo sada da po Reimovom teoremu na kružnice
. Uočimo sada da po Reimovom teoremu na kružnice 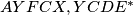 (točke
(točke  i
i  ) vrijedi da je
) vrijedi da je 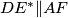 , a primjenom na kružnice
, a primjenom na kružnice 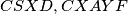 (točke
(točke  i
i  ) dobivamo da je
) dobivamo da je 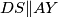 , odnosno,
, odnosno, 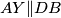 , odnosno,
, odnosno, 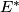 je presjek paralele kroz
je presjek paralele kroz  s
s  i paralele kroz
i paralele kroz  sa
sa  , odnosno,
, odnosno, 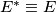 . Sada znamo da je
. Sada znamo da je  centar spiralne sličnosti koja šalje trokut
centar spiralne sličnosti koja šalje trokut 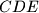 u trokut
u trokut 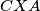 , odnosno,
, odnosno, 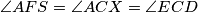 .
.
 Školjka
Školjka  ,
,  be points such that
be points such that 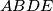 is a parallelogram. The diagonals
is a parallelogram. The diagonals  and
and 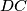 intersect at
intersect at 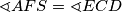 .
.