Najveći broj elemenata koje jeftin skup može imati je  . Primjer takvog skupa je
. Primjer takvog skupa je 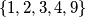 .
.
Pretpostavimo da postoji jeftin skup s  ili više članova.
ili više članova.
Promotrimo podskup od najmanja  člana skupa veća od
člana skupa veća od  . Neka
. Neka  člana tog podskupa su relativno prosti, pa postoji parem jedan par relativno prostih brojeva većih od
člana tog podskupa su relativno prosti, pa postoji parem jedan par relativno prostih brojeva većih od  u skupu. Uzmimo
u skupu. Uzmimo  relativno prosta člana skupa takva da im je suma minimalna. Neka su ti brojevi
relativno prosta člana skupa takva da im je suma minimalna. Neka su ti brojevi  i
i  . Promotrimo sada
. Promotrimo sada 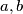 i neki broj iz skupa veći od
i neki broj iz skupa veći od  . Označimo ga s
. Označimo ga s  . Mora biti zadovoljen jedan od sljedećih uvjeta:
. Mora biti zadovoljen jedan od sljedećih uvjeta: 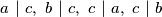 Ako
Ako 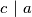 tada
tada 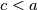 , a
, a 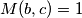 , pa
, pa 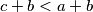 što je u kontradikciji s minimalnošću
što je u kontradikciji s minimalnošću  . Prema tome,
. Prema tome, 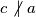 . Analogno,
. Analogno, 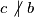 . Iz ovog slijedi da su svi članovi skupa različiti od
. Iz ovog slijedi da su svi članovi skupa različiti od 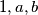 djeljivi ili s
djeljivi ili s  ili s
ili s  , a kako u skupu ima barem
, a kako u skupu ima barem  elemenata, postoje ili
elemenata, postoje ili  djeljiva s
djeljiva s  ili
ili  djeljiva s
djeljiva s  . Bez smanjenja općenitosti možemo pretpostaviti da su
. Bez smanjenja općenitosti možemo pretpostaviti da su  broja djeljiva s
broja djeljiva s  , te ih označimo s
, te ih označimo s 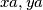 . Međutim, tada u podskupu
. Međutim, tada u podskupu 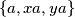 ne postoje
ne postoje  relativno prosta broja, što je kontradikcija.
relativno prosta broja, što je kontradikcija.
Zaključujemo da ne postoji jeftin skup s više od  elemenata.
elemenata.
Najveći broj elemenata koje jeftin skup može imati je $5$. Primjer takvog skupa je $\{1, 2, 3, 4, 9\}$.\\
Pretpostavimo da postoji jeftin skup s $6$ ili više članova.\\
Promotrimo podskup od najmanja $3$ člana skupa veća od $1$. Neka $2$ člana tog podskupa su relativno prosti, pa postoji parem jedan par relativno prostih brojeva većih od $1$ u skupu. Uzmimo $2$ relativno prosta člana skupa takva da im je suma minimalna. Neka su ti brojevi $a$ i $b$. Promotrimo sada $a,b$ i neki broj iz skupa veći od $1$. Označimo ga s $c$. Mora biti zadovoljen jedan od sljedećih uvjeta: $$a\ | \ c, \ b \ | \ c, \ c\ | \ a, \ c\ | \ b$$ Ako $c \ | \ a$ tada $c < a$, a $M(b,c)=1$, pa $c+b<a+b$ što je u kontradikciji s minimalnošću $a+b$. Prema tome, $c \not | \ a$. Analogno, $c \not | \ b$.
Iz ovog slijedi da su svi članovi skupa različiti od $1,a,b$ djeljivi ili s $a$ ili s $b$, a kako u skupu ima barem $6$ elemenata, postoje ili $2$ djeljiva s $a$ ili $2$ djeljiva s $b$. Bez smanjenja općenitosti možemo pretpostaviti da su $2$ broja djeljiva s $a$, te ih označimo s $xa,ya$. Međutim, tada u podskupu $\{a,xa,ya\}$ ne postoje $2$ relativno prosta broja, što je kontradikcija.
\\ \\
Zaključujemo da ne postoji jeftin skup s više od $5$ elemenata.
 . Primjer takvog skupa je
. Primjer takvog skupa je 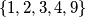 .
. ili više članova.
ili više članova. člana skupa veća od
člana skupa veća od  . Neka
. Neka  člana tog podskupa su relativno prosti, pa postoji parem jedan par relativno prostih brojeva većih od
člana tog podskupa su relativno prosti, pa postoji parem jedan par relativno prostih brojeva većih od  u skupu. Uzmimo
u skupu. Uzmimo  relativno prosta člana skupa takva da im je suma minimalna. Neka su ti brojevi
relativno prosta člana skupa takva da im je suma minimalna. Neka su ti brojevi  i
i  . Promotrimo sada
. Promotrimo sada 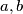 i neki broj iz skupa veći od
i neki broj iz skupa veći od  . Označimo ga s
. Označimo ga s  . Mora biti zadovoljen jedan od sljedećih uvjeta:
. Mora biti zadovoljen jedan od sljedećih uvjeta: 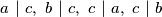 Ako
Ako 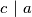 tada
tada 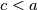 , a
, a 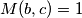 , pa
, pa 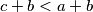 što je u kontradikciji s minimalnošću
što je u kontradikciji s minimalnošću  . Prema tome,
. Prema tome, 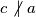 . Analogno,
. Analogno, 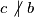 . Iz ovog slijedi da su svi članovi skupa različiti od
. Iz ovog slijedi da su svi članovi skupa različiti od 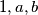 djeljivi ili s
djeljivi ili s  ili s
ili s  , a kako u skupu ima barem
, a kako u skupu ima barem  elemenata, postoje ili
elemenata, postoje ili  djeljiva s
djeljiva s  ili
ili  djeljiva s
djeljiva s  . Bez smanjenja općenitosti možemo pretpostaviti da su
. Bez smanjenja općenitosti možemo pretpostaviti da su  broja djeljiva s
broja djeljiva s  , te ih označimo s
, te ih označimo s 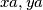 . Međutim, tada u podskupu
. Međutim, tada u podskupu 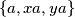 ne postoje
ne postoje  relativno prosta broja, što je kontradikcija.
relativno prosta broja, što je kontradikcija.  elemenata.
elemenata.  Školjka
Školjka