Točno
20. kolovoza 2018. 21:54 (7 godine, 6 mjeseci)
Sakrij rješenje
Neka su $x_1, x_2, \ldots, x_9$ nenegativni realni brojevi takvi da $x_1+x_2+\ldots+x_9 = 63$. Dokaži:
$$12 \leqslant \sqrt[3]{1+x_1} + \sqrt[3]{1+x_2} + \ldots + \sqrt[3]{1+x_9} \leqslant 18$$
\begin{flushright}\emph{(Ivan Sinčić)}\end{flushright}
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Dokažimo prvo da vrijedi $$\sqrt[3]{1+x_1} + \sqrt[3]{1+x_2} + \ldots + \sqrt[3]{1+x_9} \leqslant 18$$ Iz nejednakosti između kubne i aritmetičke sredine slijedi $$\sqrt[3]{1+x_1} + \sqrt[3]{1+x_2} + \ldots + \sqrt[3]{1+x_9} \leqslant 9\sqrt[3]{\frac{x_1+1+x_2+1+\ldots+x_9+1}{9}}=9\sqrt[3]{\frac{9+63}{9}} = 18$$
što je i trebalo dokazati.
Za dokaz druge strane, dokažimo prvo jednu pomoćnu lemu:
Za nenegativne realne brojeve $x,y$ vrijedi $$\sqrt[3]{x+1}+\sqrt[3]{y+1}\geqslant 1+\sqrt[3]{x+y+1}$$ Napravimo supstituciju $a=\sqrt[3]{x+1}$, $b=\sqrt[3]{y+1}$. Tvrdnja je tada ekvivalentna s $$a+b\geqslant 1+\sqrt[3]{a^3+b^3-1} \iff$$ $$(a+b-1)^3+1 \geqslant a^3+b^3 \iff $$ $$(a+b)((a+b-1)^2-(a+b-1)+1)\geqslant (a+b)(a^2+b^2-ab) \iff $$ $$ a^2+2ab+b^2-2a-2b+1-a-b+2 \geqslant a^2+b^2-ab \iff$$ $$ab+1\geqslant a+b \iff$$ $$(a-1)(b-1)\geqslant 0$$ što vrijedi jer su $a$ i $b$ veći ili jednaki $1$. \\
Uzastopnom primjenom leme dobivamo da vrijedi $$\sqrt[3]{1+x_1} + \sqrt[3]{1+x_2} + \ldots + \sqrt[3]{1+x_9}\geqslant 8+\sqrt[3]{1+x_1+x_2+\ldots+x_9}=8+\sqrt[3]{64}=12$$ što je i trebalo dokazati.
![\sqrt[3]{1+x_1} + \sqrt[3]{1+x_2} + \ldots + \sqrt[3]{1+x_9} \leqslant 18](/media/m/3/d/3/3d34335fbb916d5ef13146640b2f8b18.png) Iz nejednakosti između kubne i aritmetičke sredine slijedi
Iz nejednakosti između kubne i aritmetičke sredine slijedi ![\sqrt[3]{1+x_1} + \sqrt[3]{1+x_2} + \ldots + \sqrt[3]{1+x_9} \leqslant 9\sqrt[3]{\frac{x_1+1+x_2+1+\ldots+x_9+1}{9}}=9\sqrt[3]{\frac{9+63}{9}} = 18](/media/m/8/b/6/8b63f31f7e63adf40b6d59dd01c1b596.png) što je i trebalo dokazati.
što je i trebalo dokazati.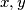 vrijedi
vrijedi ![\sqrt[3]{x+1}+\sqrt[3]{y+1}\geqslant 1+\sqrt[3]{x+y+1}](/media/m/8/0/a/80aa00fd89fd7041bafa965d4ac4160c.png) Napravimo supstituciju
Napravimo supstituciju ![a=\sqrt[3]{x+1}](/media/m/0/4/1/041d16da8d205a327077fe9a0c82fba8.png) ,
, ![b=\sqrt[3]{y+1}](/media/m/0/7/a/07a9280dc88bbc5b73cc960eee231c8d.png) . Tvrdnja je tada ekvivalentna s
. Tvrdnja je tada ekvivalentna s ![a+b\geqslant 1+\sqrt[3]{a^3+b^3-1} \iff](/media/m/9/f/5/9f570c50bfb4e80a101fac22eb26b87f.png)
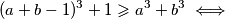
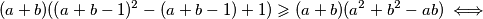
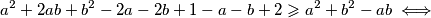
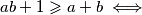
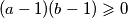 što vrijedi jer su
što vrijedi jer su  i
i  veći ili jednaki
veći ili jednaki  .
. ![\sqrt[3]{1+x_1} + \sqrt[3]{1+x_2} + \ldots + \sqrt[3]{1+x_9}\geqslant 8+\sqrt[3]{1+x_1+x_2+\ldots+x_9}=8+\sqrt[3]{64}=12](/media/m/f/d/c/fdc3dc950776149477a3443a0caa0ae8.png) što je i trebalo dokazati.
što je i trebalo dokazati.  Školjka
Školjka 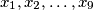 nenegativni realni brojevi takvi da
nenegativni realni brojevi takvi da 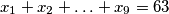 . Dokaži:
. Dokaži: ![12 \leqslant \sqrt[3]{1+x_1} + \sqrt[3]{1+x_2} + \ldots + \sqrt[3]{1+x_9} \leqslant 18](/media/m/b/3/c/b3c01db2fe544261680d6c646977f08d.png)