Neocijenjeno
20. kolovoza 2018. 21:57 (7 godine, 6 mjeseci)
Sakrij rješenje
Dan je šiljastokutni trokut $ABC$ takav da mu je $\overline{BC}$ najduža stranica. Neka je $\Gamma$ njegova opisana kružnica, a $\Omega_B$ i $\Omega_C$ kružnice središta $B$, $C$ radijusa $|BA|$, $|CA|$ redom. Dokaži da tri sjecišta kružnica $\Gamma, \Omega_B, \Omega_C$ koja nisu $A$ čine trokut sličan trokutu $ABC$.
\begin{flushright}\emph{(Borna Šimić)}\end{flushright}
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Neka je $X$ drugo sjecište $\omega_B$ i $\omega_C$, $Y$ drugo sjecište $\omega_C$ i $\Gamma$ a $Z$ drugo sjecište $\omega_B$ i $\Gamma$. Neka je $Y'$ drugo sjecište $AB$ i $\omega_C$ i $Z'$ drugo sjecište $AC$ i $\omega_B$.
Neka je $R$ refleksija preko pravca $BC$.
Imamo $R(\omega_B) = \omega_B$ i $R(\omega_C) = \omega_C$ jer su im središta na $BC$ pa je $R(A)$ drugo sjecište $\omega_B$ i $\omega_C$. Prema tome, $R(A) = X$.
Imamo $$|\angle BYC| = |\angle BZC| = |\angle BY'C| = |\angle BZ'C| = 180^{\circ} - |\angle BAC|$$
pa zbog $Y, Y' \in \omega_C$ i $Z, Z' \in \omega_B$ imamo $R(Y) = Y'$ i $R(Z) = R(Z')$ (sa svake strane $BC$ postoji točno jedna točka na kružnicama $\omega_B, \omega_C$ odgovarajućeg kuta sa $B$ i $C$).
Prema tome, $R(AB) = R(AY') = XY$ i analogno $R(AC) = XZ$ pa zbog $B, C \in BC$ imamo da su $B, Y, X$ i $C, Z, X$ kolinearne.
Primijetimo da imamo $|\angle YXZ| = |\angle BAC|$ zbog svojstava refleksije preko $BC$, te imamo:
$$|\angle XYZ| = 180^{\circ} - |\angle BYZ| = |\angle BCZ| = |\angle BCZ'| = |\angle BCA|$$
pa su trokuti $ABC$ i $XYZ$ slični.
 drugo sjecište
drugo sjecište  i
i 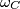 ,
,  drugo sjecište
drugo sjecište 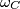 i
i  a
a  drugo sjecište
drugo sjecište  i
i  . Neka je
. Neka je 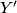 drugo sjecište
drugo sjecište  i
i 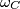 i
i 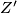 drugo sjecište
drugo sjecište  i
i  .
. refleksija preko pravca
refleksija preko pravca  . Imamo
. Imamo 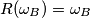 i
i 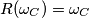 jer su im središta na
jer su im središta na  pa je
pa je 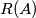 drugo sjecište
drugo sjecište  i
i 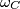 . Prema tome,
. Prema tome, 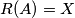 . Imamo
. Imamo 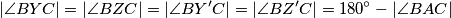 pa zbog
pa zbog 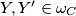 i
i 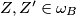 imamo
imamo 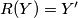 i
i 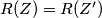 (sa svake strane
(sa svake strane  postoji točno jedna točka na kružnicama
postoji točno jedna točka na kružnicama 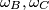 odgovarajućeg kuta sa
odgovarajućeg kuta sa  i
i  ).
).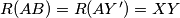 i analogno
i analogno 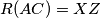 pa zbog
pa zbog 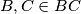 imamo da su
imamo da su 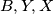 i
i 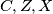 kolinearne.
kolinearne.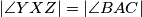 zbog svojstava refleksije preko
zbog svojstava refleksije preko  , te imamo:
, te imamo: 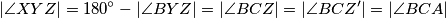 pa su trokuti
pa su trokuti  i
i 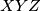 slični.
slični.  Školjka
Školjka  najduža stranica. Neka je
najduža stranica. Neka je 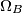 i
i 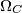 kružnice središta
kružnice središta 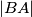 ,
, 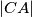 redom. Dokaži da tri sjecišta kružnica
redom. Dokaži da tri sjecišta kružnica 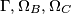 koja nisu
koja nisu  čine trokut sličan trokutu
čine trokut sličan trokutu