Kliknite ovdje kako biste prikazali rješenje.
Neka 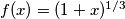 , tada
, tada 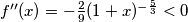 pa je
pa je  konkavna na
konkavna na 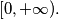 Sada, iz Jensenove nejednakosti slijedi:
Sada, iz Jensenove nejednakosti slijedi: 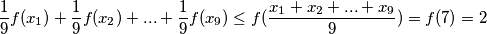 što je desna nejednakost.
što je desna nejednakost.
Lijeva nejednakost slijedi iz ove pomocne tvrdnje:
![\sqrt[3]{1+x} + \sqrt[3]{1+y} \geq \sqrt[3]{1+x+y} + 1](/media/m/f/e/6/fe66d1d6a722055c73e3e295c50e024b.png)
gdje su 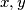 nenegativni realni brojevi. Nadalje jednakost se postize ako i samo ako je
nenegativni realni brojevi. Nadalje jednakost se postize ako i samo ako je 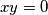 .
.
Dokaz:
Pretpostavimo da su  oba pozitivni . Neka
oba pozitivni . Neka ![L = \sqrt[3]{1+x} + \sqrt[3]{1+y}](/media/m/c/f/4/cf4b437ffc6ecdaaf4aa5b9e320cc99f.png) i
i ![R=\sqrt[3]{1+x+y}+1](/media/m/6/9/4/69451585d27c1ec569c1d519093c7b83.png) . Neka je niz
. Neka je niz 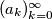 zadan sa:
zadan sa: 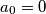 ,
, 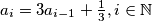 . Takoder neka
. Takoder neka 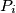 oznacava tvrdnju da
oznacava tvrdnju da ![[(1+x)(1+y)]^{a_i}L > (1+x+y)^{a_i}R](/media/m/b/2/2/b2263f81add5e21b772bc9a2aed2aeee.png) .
.
Primijetimo da je 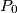 tocno tvrdnja koju zelim dokazati. Plan je dokazati da
tocno tvrdnja koju zelim dokazati. Plan je dokazati da 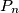 vrijedi za neki veliki
vrijedi za neki veliki  te dokazati implikaciju
te dokazati implikaciju 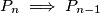 gdje je
gdje je  cime cu naravno dobiti i
cime cu naravno dobiti i 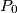 . Za fiksni par
. Za fiksni par 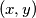 pozitivnih realnih brojeva vrijedi:
pozitivnih realnih brojeva vrijedi: 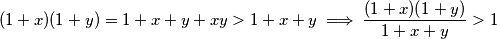 Niz
Niz 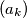 je strogo rastuci i neomeden sto znaci da je za dovoljno veliki
je strogo rastuci i neomeden sto znaci da je za dovoljno veliki  :
: ![[\frac{(1+x)(1+y)}{1+ x + y}]^{a_n} > \frac{R}{L}](/media/m/6/d/2/6d2c2ce3e9f4c95d77d1730c08d9f53d.png) Preostaje
Preostaje 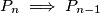 . Iz
. Iz 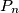 :
:
![3[(1+x)(1+y)]^{3a_{n-1}}( [(1+x)(1+y)]^{\frac{1}{3}}L ) > 3 (1+x+y)^{3a_{n-1}}((1+x+y)^{\frac{1}{3}} R)](/media/m/e/f/3/ef3c1e7b80e18d8facd17da5ad362004.png) Vrijedi (jer je
Vrijedi (jer je 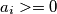 za
za  nenegativan):
nenegativan): ![[(1+x)(1+y)]^{3a_{n-1}}(2+x+y) \geq (1+x+y)^{3a_{n-1}}(2+x+y)](/media/m/0/3/9/03995db86d383c159f9602f8bb2e9349.png) Zbrajanjem:
Zbrajanjem: ![[(1+x)(1+y)]^{3a_{n-1}}(1+x+3[(1+x)(1+y)]^{\frac{1}{3}}L +1+y) > (1+x+y)^{3a_{n-1}}(1+x+y+3(1+x+y)^{\frac{1}{3}} R+1)](/media/m/6/7/2/6721a3fca6865ce6a7d4c0de1f34c928.png) Sto je isto kao:
Sto je isto kao: ![[(1+x)(1+y)]^{3a_{n-1}}L^3 > (1+x+y)^{3a_{n-1}}R^3](/media/m/a/0/0/a007b92530a21705c0722188a4b2bce5.png) Pa uzimanjem treceg korijena slijedi:
Pa uzimanjem treceg korijena slijedi: ![[(1+x)(1+y)]^{a_{n-1}}L > (1+x+y)^{a_{n-1}}R](/media/m/6/5/6/6567bd485bb18007ca51c7738b03b5cf.png) Ovo je upravo
Ovo je upravo 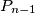 pa smo gotovi.
pa smo gotovi.
 Školjka
Školjka 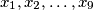 nenegativni realni brojevi takvi da
nenegativni realni brojevi takvi da 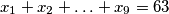 . Dokaži:
. Dokaži: ![12 \leqslant \sqrt[3]{1+x_1} + \sqrt[3]{1+x_2} + \ldots + \sqrt[3]{1+x_9} \leqslant 18](/media/m/b/3/c/b3c01db2fe544261680d6c646977f08d.png)
![R = \sqrt[3]{1+x+y} + 1](/media/m/3/0/5/305cfc1d47d946ed47ada824536b0543.png) , iz one leme ne dobiješ traženu nejednakost (moguće da ako ponoviš dokaz možeš dobit ovu lemu koja rješava zadatak, nisam pogledao tvoj dokaz leme za
, iz one leme ne dobiješ traženu nejednakost (moguće da ako ponoviš dokaz možeš dobit ovu lemu koja rješava zadatak, nisam pogledao tvoj dokaz leme za ![R = \sqrt[3]{1+x+y}](/media/m/c/4/f/c4f8ec737875f8a4e64f19c15c4cd6ee.png) ).
).