Kliknite ovdje kako biste prikazali rješenje.
Uvrštavanjem 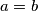 u uvjet dobivamo da za
u uvjet dobivamo da za 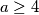 vrijedi
vrijedi 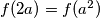 . Iz toga slijedi
. Iz toga slijedi 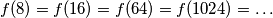 te vidimo da je
te vidimo da je 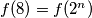 za beskonačno mnogo
za beskonačno mnogo 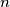 .
.
Pokažimo sada da je 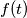 (gdje
(gdje 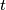 nije potencija od
nije potencija od 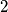 ) jednak
) jednak 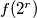 za neki
za neki  . Kada dokažemo tu tvrdnju preostat će samo dokazati da je
. Kada dokažemo tu tvrdnju preostat će samo dokazati da je 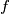 od svake potencije broja
od svake potencije broja 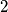 jednak
jednak 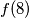 . Tvrdnju dokazujemo na način da ćemo
. Tvrdnju dokazujemo na način da ćemo 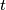 prikazati u binarnom zapisu i pokazati da možemo smanjiti broj jedinica u tom zapisu i time će na kraju ostati samo jedna jedinica što će značiti da smo dobili potenciju broja
prikazati u binarnom zapisu i pokazati da možemo smanjiti broj jedinica u tom zapisu i time će na kraju ostati samo jedna jedinica što će značiti da smo dobili potenciju broja 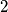 . Dakle, neka je
. Dakle, neka je 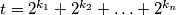 gdje je
gdje je 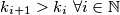 ,
, 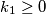 ,
, 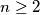 . Zbog
. Zbog 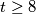 vrijedi
vrijedi 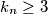 i imamo nekoliko slučaja:
i imamo nekoliko slučaja:
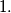
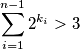 . Vrijedi:
. Vrijedi: 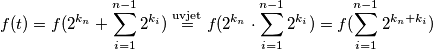 Argument zadnjeg
Argument zadnjeg 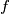 -a binaran je zapis koji sadržava
-a binaran je zapis koji sadržava 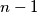 članova pa smo u ovom slučaju pokazali da možemo smanjiti broj jedinica.
članova pa smo u ovom slučaju pokazali da možemo smanjiti broj jedinica.
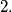
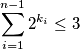 . Vrijedi:
. Vrijedi: 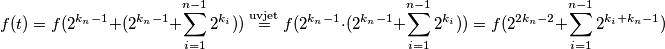
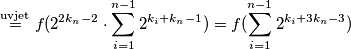 Argument zadnjeg
Argument zadnjeg 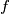 -a binaran je zapis koji sadržava
-a binaran je zapis koji sadržava 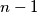 članova pa smo u ovom slučaju pokazali da možemo smanjiti broj jedinica. U oba slučaja korištenja uvjeta zadatka to je bilo u redu zbog
članova pa smo u ovom slučaju pokazali da možemo smanjiti broj jedinica. U oba slučaja korištenja uvjeta zadatka to je bilo u redu zbog 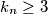 .
.
Sada smo dokazali da je svaki 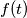 jednak nekom
jednak nekom 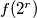 te preostaje dokazati da je
te preostaje dokazati da je 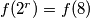 za svaki
za svaki 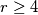 . Primijetimo sljedeće: ako imamo
. Primijetimo sljedeće: ako imamo 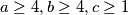 , vrijedi
, vrijedi 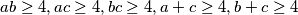 te slijedi:
te slijedi: 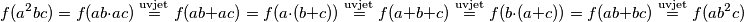 Uvrštavajući
Uvrštavajući 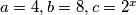 gdje je
gdje je 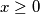 imamo:
imamo: 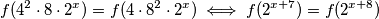 Iz čega kad uvrstimo
Iz čega kad uvrstimo 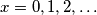 dobivamo
dobivamo 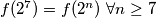 , pa je
, pa je 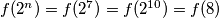 . Ostaje pokazati da je
. Ostaje pokazati da je 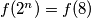 za
za 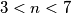 i tada smo gotovi jer smo pokazali da je
i tada smo gotovi jer smo pokazali da je 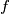 od svakog broja jednak
od svakog broja jednak 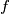 -u neke potencije broja
-u neke potencije broja 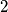 , a
, a 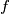 svake potencije broja
svake potencije broja 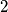 jednak
jednak 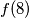 . Već smo pokazali
. Već smo pokazali 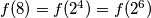 pa još moramo samo ručno pokazati
pa još moramo samo ručno pokazati 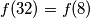 :
: 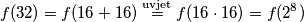 i sada smo gotovi jer već imamo
i sada smo gotovi jer već imamo 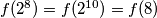 . Q.E.D.
. Q.E.D.
 Školjka
Školjka 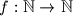 funkcija takva da je
funkcija takva da je 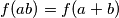 za sve prirodne brojeve
za sve prirodne brojeve 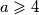 i
i 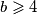 . Dokaži da je
. Dokaži da je 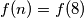 za sve prirodne brojeve
za sve prirodne brojeve 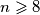 .
.