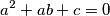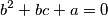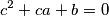Kliknite ovdje kako biste prikazali rješenje.
Primijetimo najprije da je svaka sljedeća jednadžba dobivena iz prethodne cikličnom rotacijom varijabli 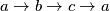 . To znači da kada dobijemo neku jednakost iz jedne ili dvije jednadžbe, smijemo primijeniti ciklični umnožak ili cikličnu sumu na obje strane jer analognu jednakost možemo dobiti iz drugih jednadžba i te jednakosti se mogu množiti i zbrajati.
. To znači da kada dobijemo neku jednakost iz jedne ili dvije jednadžbe, smijemo primijeniti ciklični umnožak ili cikličnu sumu na obje strane jer analognu jednakost možemo dobiti iz drugih jednadžba i te jednakosti se mogu množiti i zbrajati.
Iz prve jednadžbe slijedi 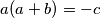 , pa uzimajući ciklični umnožak ove jednakosti dobivamo:
, pa uzimajući ciklični umnožak ove jednakosti dobivamo: 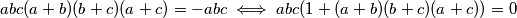 Prvi slučaj - neka od varijabla je jednaka nuli (BSO
Prvi slučaj - neka od varijabla je jednaka nuli (BSO 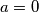 ): Iz prve jednadžbe dobivamo
): Iz prve jednadžbe dobivamo 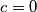 i onda lagano slijedi
i onda lagano slijedi 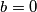 te imamo prvo rješenje
te imamo prvo rješenje 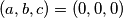
Drugi slučaj - 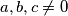 : Slijedi
: Slijedi 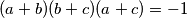 . Oduzimajući drugu jednadžbu od prve slijedi
. Oduzimajući drugu jednadžbu od prve slijedi 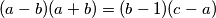 te uzimajući ciklični umnožak ove jednakosti dobivamo:
te uzimajući ciklični umnožak ove jednakosti dobivamo: 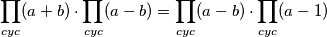
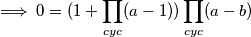 Prvi slučaj - neke dvije varijable su jednake (BSO
Prvi slučaj - neke dvije varijable su jednake (BSO 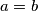 ): Iz jednakosti koju smo dobili kad smo oduzeli drugu jednadžbu od prve slijedi ili
): Iz jednakosti koju smo dobili kad smo oduzeli drugu jednadžbu od prve slijedi ili 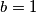 (iz čega je onda
(iz čega je onda 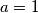 te lako dobivamo da to nije rješenje) ili ako
te lako dobivamo da to nije rješenje) ili ako 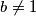 mora biti
mora biti  pa su sve tri varijable jednake. U tom drugom podslučaju iz prve jednadžbe slijedi
pa su sve tri varijable jednake. U tom drugom podslučaju iz prve jednadžbe slijedi 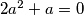 i kako već imamo
i kako već imamo 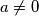 dobivamo drugo rješenje zadatka
dobivamo drugo rješenje zadatka 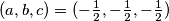 .
.
Drugi slučaj - nikoje dvije varijable nisu međusobno jednake: Slijedi 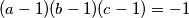 . Prva jednadžba se također može zapisati kao
. Prva jednadžba se također može zapisati kao 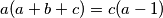 , pa uzimajući ciklični umnožak te jednakosti dobivamo:
, pa uzimajući ciklični umnožak te jednakosti dobivamo: 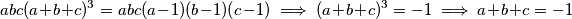 Koristeći dobivenu tvrdnju u preuređenoj prvoj jednadžbi koju smo upravo iskoristili dobivamo
Koristeći dobivenu tvrdnju u preuređenoj prvoj jednadžbi koju smo upravo iskoristili dobivamo  te analogno zbog cikličnosti iz drugih jednadžba slijedi
te analogno zbog cikličnosti iz drugih jednadžba slijedi 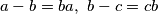 . Te tri jednakosti se također mogu zapisati kao:
. Te tri jednakosti se također mogu zapisati kao: 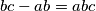
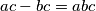
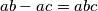 Zbrajajući ih dobivamo
Zbrajajući ih dobivamo 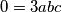 što je u kontradikciji s time da su sve tri varijable različite od
što je u kontradikciji s time da su sve tri varijable različite od 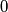 pa su jedina rješenja
pa su jedina rješenja 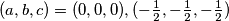 .
.
 Školjka
Školjka 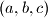 of real numbers satisfying the system of equations
of real numbers satisfying the system of equations