Točno
24. studenoga 2018. 15:30 (7 godine, 2 mjeseci)
Let

be the orthocenter of an acute-angled triangle

. The circle
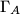
centered at the midpoint of

and passing through

intersects the sideline

at points
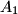
and
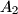
. Similarly, define the points
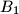
,
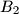
,
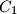
and
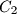
.
Prove that six points
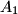
,
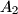
,
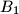
,
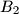
,
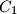
and
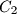
are concyclic.
Author: Andrey Gavrilyuk, Russia
%V0
Let $H$ be the orthocenter of an acute-angled triangle $ABC$. The circle $\Gamma_{A}$ centered at the midpoint of $BC$ and passing through $H$ intersects the sideline $BC$ at points $A_{1}$ and $A_{2}$. Similarly, define the points $B_{1}$, $B_{2}$, $C_{1}$ and $C_{2}$.
Prove that six points $A_{1}$ , $A_{2}$, $B_{1}$, $B_{2}$, $C_{1}$ and $C_{2}$ are concyclic.
Author: Andrey Gavrilyuk, Russia
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Po definiciji točke leže na drugoj Droz-Farny kružnici trokuta.
Po definiciji točke leže na drugoj Droz-Farny kružnici trokuta.