Točno
29. rujna 2018. 22:49 (5 godine, 6 mjeseci)
Nađite sve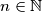 
za koje je izraz 
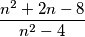cijeli broj.
Nađite sve $n\in\mathbb{N}$ za koje je izraz $\dfrac{n^2+2n-8}{n^2-4}$ cijeli broj.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
(n^2 - 4 + 2n - 4)/((n-2)(n+2) = 1 + 2(n-2)/(n-2)(n+2) = 1 + 2/(n+2) Kako ne postoji takav n iz N da je 2/(n+2) cijeli broj, onda ne postoji ni jedan takav n.
(n^2 - 4 + 2n - 4)/((n-2)(n+2)
= 1 + 2(n-2)/(n-2)(n+2)
= 1 + 2/(n+2)
Kako ne postoji takav n iz N da je 2/(n+2) cijeli broj, onda ne postoji ni jedan takav n.
| 30. rujna 2018. 07:15 | ikicic | Točno |
Školjka