Školjka
Tečajevi
MetaMath '24
Izbornik
Početna
Arhiva zadataka
Predavanja
Natjecanja
Tečajevi
Registracija
Prijava
Svi zadaci
Rješenja
Traži
Pomoć
O nama
Točno
16. ožujka 2013. 22:04 (11 godine, 11 mjeseci)
Korisnik:
mimaro
Zadatak:
skakavac 2013 drugo kolo ss1 4
(Sakrij tekst zadatka)
Dokažite da ni za koji prirodni broj
brojevi
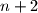
i
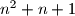
ne mogu istovremeno biti potpuni kubovi.
%V0 Dokažite da ni za koji prirodni broj $n$ brojevi $n + 2$ i $n^2 + n + 1$ ne mogu istovremeno biti potpuni kubovi.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Pretpostavimo da mogu, ali tada je
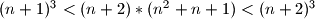
. Kontradikcija!
%V0 Pretpostavimo da mogu, ali tada je $(n+1)^3 < (n+2)*(n^2 +n +1) < (n+2)^3$. Kontradikcija!
Ocjene: (1)
17. ožujka 2013. 18:20
grga
Točno
Školjka 
brojevi 
i 
ne mogu istovremeno biti potpuni kubovi. 
. Kontradikcija!