Točno
16. ožujka 2013. 22:10 (12 godine, 11 mjeseci)
Dokažite da za bilo koje pozitivne brojeve

,

,

i bilo koji nenegativan pozitivan broj

vrijedi nejednakost
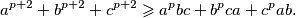
%V0
Dokažite da za bilo koje pozitivne brojeve $a$, $b$, $c$ i bilo koji nenegativan pozitivan broj $p$ vrijedi nejednakost $$a^{p+2} + b^{p+2} + c^{p+2} \geqslant a^pbc + b^pca + c^pab \text{.}$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Primijetimo da zamjenom

i

dobivamo istu nejednakost. Sada možemo uzeti
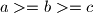
, a primjenom Teorema malog Ivice na jednako uređene nizove
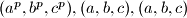
dobivamo traženu nejednakost.
%V0
Primijetimo da zamjenom $a$ i $b$ dobivamo istu nejednakost. Sada možemo uzeti $a>=b>=c$, a primjenom Teorema malog Ivice na jednako uređene nizove $(a^p, b^p, c^p), (a,b,c), (a,b,c)$ dobivamo traženu nejednakost.
| 17. ožujka 2013. 10:55 | ikicic | Točno |
| 17. ožujka 2013. 18:20 | grga | Točno |