Neka je  konveksan četverokut takav da
konveksan četverokut takav da  nije paralelno s
nije paralelno s  . Neka je
. Neka je  presjek njegovih dijagonala, a
presjek njegovih dijagonala, a  presjek pravaca
presjek pravaca  i
i  . Pretpostavimo da u unutrašnjosti
. Pretpostavimo da u unutrašnjosti  postoji točka
postoji točka  takva da njezine projekcije na stranice
takva da njezine projekcije na stranice  čine pravokutnik. Neka je opisana kružnica tog pravokutnika
čine pravokutnik. Neka je opisana kružnica tog pravokutnika  .
.  i
i  su sjecišta
su sjecišta  s
s  i
i  , redom.
, redom.  je presjek tangenta na
je presjek tangenta na  u
u  i
i  . Dokažite da
. Dokažite da  leži na pravcu
leži na pravcu  .
.
Kliknite ovdje kako biste prikazali rješenje.
Oznacimo vrhove pravokutnika sa  ,
,  ,
,  I
I 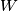 tako da
tako da  lezi na
lezi na  ,
,  na
na  ,
,  na
na  i
i 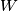 na
na 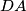 .
.
Laganim angle chasom dobijemo 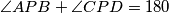 pa
pa  ima izogonalnu konjugatu s obzirom na cetverokut
ima izogonalnu konjugatu s obzirom na cetverokut  , oznacimo tu točku sa
, oznacimo tu točku sa 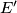 .
.
Imamo 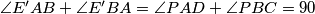 . Analogno dobijemo
. Analogno dobijemo 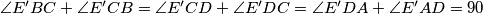 pa vrijedi
pa vrijedi 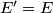 .
.
Uocimo da su  i E takoder izogonalne konjugate u
i E takoder izogonalne konjugate u 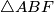 .
.
S obzirom da u svakom trokutu vrijedi da su projekcije izogonalnih konjugata na stranice trokuta konciklicne, imamo da su  i
i  zapravo projekcije tocke
zapravo projekcije tocke  na
na 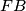 i
i 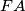 pa
pa 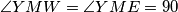 i
i 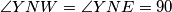 pa
pa  takoder lezi na
takoder lezi na 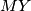 i
i 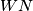 .
.
Sada imamo da je 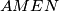 tetivan i promjer kružnice je
tetivan i promjer kružnice je  .
.
Iz 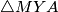 imamo
imamo 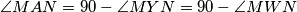 (ovdje pretpostavljamo
(ovdje pretpostavljamo  , ali drugi slučaj se rjesi analogno), no iz toga sto su
, ali drugi slučaj se rjesi analogno), no iz toga sto su 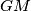 i
i 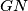 tangente iz G na k imamo
tangente iz G na k imamo 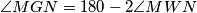 .
.
Slijedi da je  središte kruznice opisane cetverokutu
središte kruznice opisane cetverokutu 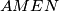 tj.
tj.  ,
,  i
i  su kolinearne.
su kolinearne.
 Školjka
Školjka