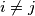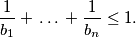Definiramo: $X_i = b_iA+c_i$, $f(x) = | \{ y \leq x : y \in A \} |$, $\phi_i(x) = | \{ y \leq x : y \in X_i \} |$
Vrijedi: $\phi_i(x) = f( \frac{x-c_i}{b_i})$
Prvo primijetimo da je svaki od $X_i$ pa i $A$ beskonačan i promatrajmo slučaj kada $b_i=1$ za neki $i$, WLOG $i=1$:
Ako je $n=1$ tvrdnja zadatka vrijedi. Inače za $n\geq 2$ po D.P u $X_2$ postoje dva elementa koji su isti mod $c_1$, neka su to $u<v$.
Sada vrijedi $u+kc_1 \in X_1$ što povlači da je $v \in X_1 \Rightarrow\!\Leftarrow$ (jer su $X_1$ i $X_2$ disjunktni)
Dalje promatramo kada $b_i \geq 2 \ \forall i$. Pretpostavimo suprotno tvrdnji zadatka.
Zbog disjunktnosti vrijedi $f(x) \geq \sum_{i=1}^{n} \phi_i(x)$, dakle $$\sum \frac{\phi_i(x)}{f(x)} \leq 1 < \sum \frac{1}{b_i}$$ (uzmemo $x$ dovoljno velik da $f(x)$ nije 0). Slijedi: $\sum \frac{\phi_i(x)}{f(x)} - \frac{1}{b_i} < 0$, tj. postoji indeks $i_1$ za koji je $\frac{\phi_{i_1}(x)}{f(x)} - \frac{1}{b_{i_1}} < 0$ što je ekvivalentno s: $$f(x) > b_{i_1} f(\frac{x-c_{i_1}}{b_{i_1}})$$
Neka je $x_1 = \frac{x-c_{i_1}}{b_{i_1}}$. Za taj $x_1$ možemo naći odgovarajući indeks $i_2$ i definirati $x_2$ i tako dalje. Prestajemo kad je $x_k < M$ prvi put za neki pozitivan broj $M$ koji uzmemo tako da možemo garantirati da $x_k$ nije premali tj. $f(x_k)>0$. Vrijedi niz nejednakosti:
$$f(x) > b_{i_1} f(x_1)$$
$$f(x_1) > b_{i_2}f(x_2) ...$$
$$f(x_{k-1}) > b_{i_k}f(x_k)$$
Kombinirajući: $f(x) > b_{i_1}b_{i_2}...b_{i_k} f(x_k) \geq b_{i_1}b_{i_2}...b_{i_k}$ ili $\frac{f(x)}{x} > \frac{b_{i_1}b_{i_2}...b_{i_k}}{x}$.
Uvrštavajući se dobije: $$x_k = \frac{x-c_{i_1}-b_{i1}c_{i2}-...-b_{i_1}b_{i_2}...b_{i_{k-1}}c_{i_k}}{b_{i_1}b_{i_2}...b_{i_k}} < M \implies$$
$$\frac{x}{b_{i_1}b_{i_2}...b_{i_k}} \leq M + \frac{c_{i_k}}{b_{i_k}} + \frac{c_{i_{k-1}}}{b_{i_{k-1}}b_{i_k}}+...+\frac{c_{i_1}}{b_{i_1}b_{i_2}...b_{i_k}}$$
Neka je $c$ maksimalna vrijednost $c_i$ i $b$ minimalna vrijednost $b_i$, tada imamo:
$$\frac{x}{b_{i_1}b_{i_2}...b_{i_k}} \leq M + c(\frac{1}{b} + \frac{1}{b^2}+...+\frac{1}{b^k}) < M + c(\frac{1}{b} + \frac{1}{b^2}+...) = M+\frac{c}{b-1}$$
Slijedi da je za velike $x$:
$$\frac{f(x)}{x} > \frac{b_{i_1}b_{i_2}...b_{i_k}}{x} > \frac{1}{M+\frac{c}{b-1}}$$ iz čega slijedi: $$\varliminf_{x \to \infty} \frac{f(x)}{x} = \beta > 0$$
$$\varliminf_{x \to \infty} \frac{\phi_i(x)}{x} = \varliminf_{x \to \infty} \frac{f(\frac{x-c_i}{b_i})}{\frac{x-c_i}{b_i}}\frac{x-c_i}{x} \frac{1}{b_1} = \frac{\beta}{b_i}$$
Sada iz $f(x) \geq \sum_{i=1}^{n} \phi_i(x) \implies \frac{f(x)}{x} \geq \sum_{i=1}^{n} \frac{\phi_i(x)}{x}$
Možemo uzeti limes infimum s obe strane i očuva se nejednakost:
$$\varliminf_{x \to \infty} \frac{f(x)}{x} = \beta \geq \varliminf_{x \to \infty}\sum_{i=1}^{n} \frac{\phi_i(x)}{x} $$
Svojstva limes infimuma nam dopuštaju i da "izvučemo" sumu:
$$\varliminf_{x \to \infty}\sum_{i=1}^{n} \frac{\phi_i(x)}{x} \geq \sum_{i=1}^{n} \varliminf_{x \to \infty} \frac{\phi_i(x)}{x} = \sum_{i=1}^{n} \frac{\beta}{b_i}$$
Napokon slijedi: $$\beta \geq \sum_{i=1}^{n} \frac{\beta}{b_i} \implies 1 \geq \sum_{i=1}^{n} \frac{1}{b_i}$$
Ovo kontradiktira pretpostavku da tvrdnja zadataka ne vrijedi pa smo gotovi.
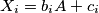 ,
, 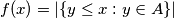 ,
, 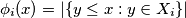
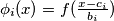
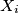 pa i
pa i  beskonačan i promatrajmo slučaj kada
beskonačan i promatrajmo slučaj kada 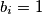 za neki
za neki  , WLOG
, WLOG 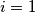 :
: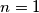 tvrdnja zadatka vrijedi. Inače za
tvrdnja zadatka vrijedi. Inače za 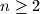 po D.P u
po D.P u 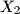 postoje dva elementa koji su isti mod
postoje dva elementa koji su isti mod 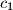 , neka su to
, neka su to 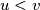 . Sada vrijedi
. Sada vrijedi 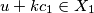 što povlači da je
što povlači da je 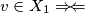 (jer su
(jer su 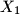 i
i 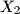 disjunktni)
disjunktni)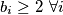 . Pretpostavimo suprotno tvrdnji zadatka.
. Pretpostavimo suprotno tvrdnji zadatka.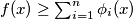 , dakle
, dakle 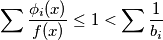 (uzmemo
(uzmemo  dovoljno velik da
dovoljno velik da 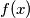 nije 0). Slijedi:
nije 0). Slijedi: 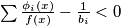 , tj. postoji indeks
, tj. postoji indeks 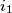 za koji je
za koji je 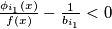 što je ekvivalentno s:
što je ekvivalentno s: 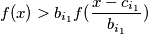
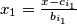 . Za taj
. Za taj 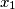 možemo naći odgovarajući indeks
možemo naći odgovarajući indeks 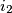 i definirati
i definirati 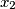 i tako dalje. Prestajemo kad je
i tako dalje. Prestajemo kad je 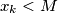 prvi put za neki pozitivan broj
prvi put za neki pozitivan broj  koji uzmemo tako da možemo garantirati da
koji uzmemo tako da možemo garantirati da 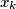 nije premali tj.
nije premali tj. 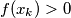 . Vrijedi niz nejednakosti:
. Vrijedi niz nejednakosti: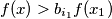
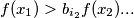
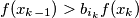
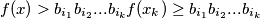 ili
ili 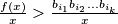 . Uvrštavajući se dobije:
. Uvrštavajući se dobije: 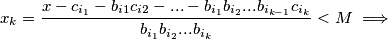
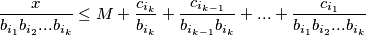 Neka je
Neka je  maksimalna vrijednost
maksimalna vrijednost 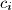 i
i  minimalna vrijednost
minimalna vrijednost 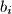 , tada imamo:
, tada imamo: 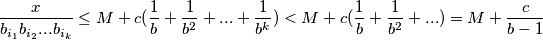
 :
: 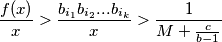 iz čega slijedi:
iz čega slijedi: 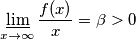
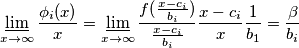
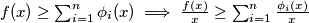 Možemo uzeti limes infimum s obe strane i očuva se nejednakost:
Možemo uzeti limes infimum s obe strane i očuva se nejednakost: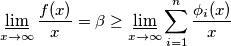
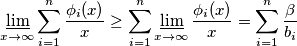
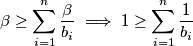
 Školjka
Školjka 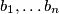 and
and 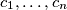 such that
such that 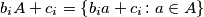 is a subset of
is a subset of 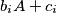 and
and 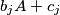 are disjoint whenever
are disjoint whenever