Neocijenjeno
11. svibnja 2019. 16:49 (6 godine, 10 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Razmotriti ćemo 3 slučaja;
1.f(n) je strogo rastuća Primjetimo ako je f(n+1) > f(f(n)) tada bi moralo i n+1 > f(n),dakle sve funkcije su oblika f(n) = n + k, gdje je k bilo koji R broj,uvrstimo novi oblik u nejednakost vidimo da je 1 > k,pošto f ide iz prirodnih brojeva u prirodne brojeve to znamo da je jedina mogućnost za naše k = 0. Tj. naša jedina funkcija koja ima osobinu da je f(n+1) > f(f(n)) je f(n) = n.
2.f(n) je strogo opadajuća Nejednakost nema riješenja,a ni smisla kad je f(n) opadajuća.
3.f(n) nije ni jedno ni drugo Nemoguće jer nejednakost ne bi važila za svako prirodno n.
Dakle jedino riješenje jeste f(n) = n, za svako prirodno n.
 Školjka
Školjka 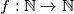 satisfying following condition:
satisfying following condition: